题目内容
6.设X={$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{4}$,$\frac{1}{5}$},若集合G⊆X,定义G中所有元素之乘积为集合G的“积数”(单元素集合的“积数”是这个元素本身),则集合X的所有非空子集的“积数”的总和为2.分析 由题意,列出所有“积数”并求和.
解答 解:由题意,
集合X的所有非空子集的“积数”之和为:
$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$+$\frac{1}{2}$×($\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$)+$\frac{1}{3}$×($\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{5}$)+$\frac{1}{4}$×($\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{5}$)+$\frac{1}{5}$×($\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$)+$\frac{1}{2}$×($\frac{1}{3}$×$\frac{1}{4}$+$\frac{1}{3}$×$\frac{1}{5}$+$\frac{1}{4}$×$\frac{1}{5}$)+$\frac{1}{3}$×($\frac{1}{3}$×$\frac{1}{4}$+$\frac{1}{4}$×$\frac{1}{5}$+$\frac{1}{3}$×$\frac{1}{5}$)+$\frac{1}{4}$×($\frac{1}{2}$×$\frac{1}{3}$+$\frac{1}{2}$×$\frac{1}{5}$+$\frac{1}{3}$×$\frac{1}{5}$)+$\frac{1}{5}$×($\frac{1}{2}$×$\frac{1}{3}$+$\frac{1}{2}$×$\frac{1}{4}$+$\frac{1}{3}$×$\frac{1}{4}$)+$\frac{1}{2}$×$\frac{1}{3}$×$\frac{1}{4}$×$\frac{1}{5}$=2.
故答案是:2.
点评 本题考查了集合的子集的列举,属于基础题.

| A. | (-1,3) | B. | (-1,1) | C. | (1,2) | D. | (2,3) |
| A. | (±4,0) | B. | (±2,0) | C. | (0,±4) | D. | (0,±2) |
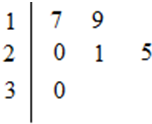 某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.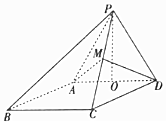 如图,四棱锥P-ABCD,底面ABCD是∠ABC=60°的菱形,侧面PAD是边长为2的正三角形,O是AD的中点,M为PC的中点.
如图,四棱锥P-ABCD,底面ABCD是∠ABC=60°的菱形,侧面PAD是边长为2的正三角形,O是AD的中点,M为PC的中点.