题目内容
已知圆 被
被 轴,
轴, 轴截得的弦长都是
轴截得的弦长都是 ,且圆心
,且圆心 在直线
在直线 上
上
设 是动圆
是动圆 :
: 的动点,
的动点, 切圆
切圆
于 两点,求圆
两点,求圆 的方程及
的方程及 的最大值和最小值
的最大值和最小值
 被
被 轴,
轴, 轴截得的弦长都是
轴截得的弦长都是 ,且圆心
,且圆心 在直线
在直线 上
上设
 是动圆
是动圆 :
: 的动点,
的动点, 切圆
切圆
于
 两点,求圆
两点,求圆 的方程及
的方程及 的最大值和最小值
的最大值和最小值最大值为 ,最小值为
,最小值为
 ,最小值为
,最小值为
设圆心 ,半径为
,半径为 ,则
,则
 ,且
,且
解得 ,由
,由 得
得 ,圆
,圆 的方程为
的方程为
即 ,设∠
,设∠
 ∠
∠ ,则∠
,则∠ ,且
,且 (*)
(*)
设 ,
, ,
, ,
,


所以 ,
, ,由
,由


由 得
得 ,
,

所以 的最大值为
的最大值为 ,最小值为
,最小值为
 ,半径为
,半径为 ,则
,则
 ,且
,且
解得
 ,由
,由 得
得 ,圆
,圆 的方程为
的方程为
即
 ,设∠
,设∠
 ∠
∠ ,则∠
,则∠ ,且
,且 (*)
(*)设
 ,
, ,
, ,
,

所以
 ,
, ,由
,由


由
 得
得 ,
,

所以
 的最大值为
的最大值为 ,最小值为
,最小值为

练习册系列答案
相关题目
 为⊙
为⊙ 中的弦,弧
中的弦,弧 为
为 ,弧
,弧 且
且 ,
, ,求半径
,求半径
 的弦
的弦 、
、 相交于点
相交于点 ,
, 的度数为
的度数为 ,
, 的度数为
的度数为 ,
, ( ).
( ).


 为前n个圆的面积之和,则
为前n个圆的面积之和,则



 相交的所有直线中,被圆截得的弦最长时的直线方程是 .
相交的所有直线中,被圆截得的弦最长时的直线方程是 .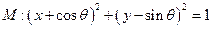 ,直线
,直线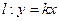 ,给出下列命题:
,给出下列命题: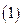 对任意实数
对任意实数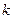 与
与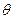 ,直线
,直线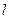 和圆
和圆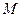 相切;
相切; 对任意实数
对任意实数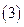 对任意实数
对任意实数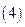 对任意实数
对任意实数 的直线交圆
的直线交圆 于点
于点 ,若
,若 ,则实数
,则实数 _______
_______  切
切 于点
于点 ,割线
,割线 经过圆心
经过圆心 ,弦
,弦 于点
于点 。已知
。已知 ,
, 则
则 。
。 。
。