题目内容
5.已知函数f(x)=Asin(ωx+φ)+B,(A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)在区间($\frac{π}{2}$,$\frac{3π}{2}$)上单调,当x=$\frac{π}{2}$时,f(x)取得最大值5,当x=$\frac{3π}{2}$时,f(x)取得最小值-1,(1)求f(x)的解析式
(2)当x∈[0,4π]时,函数g(x)=2x|f(x)|-(a+1)2x+1有8个零点,求实数a的取值范围.
分析 (1)根据函数的单调性和最值性,建立方程关系进行求解即可.
(2)利用函数与方程之间的关系进行转化,利用数形结合进行求解即可.
解答 (1)解:由题意可知,A+B=5,-A+B=-1,∴A=3,B=2
∵$\frac{2π}{ω}=2(\frac{3π}{2}-\frac{π}{2})$∴ω=1∴f(x)=3sin(x+φ)+2
又∵$f(\frac{π}{2})=5,即sin(\frac{π}{2}+φ)=1且|φ|<\frac{π}{2}∴φ=0$
∴f(x)的解析式为f(x)=3sinx+2
(2)当x∈[0,4π]时,函数g(x)有8个零点,
∵2x>0,∴原方程等价于当x∈[0,4π]时,方程|f(x)|=2(a+1)有8个不同的解.
即y=|f(x)|与y=2(a+1)有8个不同的交点.画出对应的图象,如图所示: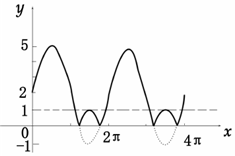
则0<2(a+1)<1,解得$-1<a<-\frac{1}{2}$
所以实数a的取值范围时$-1<a<-\frac{1}{2}$
点评 本题主要考查三角函数解析式的求解以及函数与方程的应用,求出函数的解析式以及利用数形结合是解决本题的关键.

练习册系列答案
相关题目
7.已知圆的半径为π,则60°圆心角所对的弧长为( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{{π}^{2}}{3}$ | D. | $\frac{2{π}^{2}}{3}$ |
8.已知$sin(α+\frac{13π}{6})+cosα=-\frac{1}{3}$,则$cos(\frac{π}{6}-α)$=( )
| A. | $-\frac{{2\sqrt{2}}}{3}$ | B. | $\frac{{2\sqrt{2}}}{3}$ | C. | $-\frac{{\sqrt{3}}}{9}$ | D. | $\frac{{\sqrt{3}}}{9}$ |