题目内容
若实数x、y、z满足x＋2y＋3z＝a(a为常数)，求x2＋y2＋z2的最小值．
解：∵ (12＋22＋32)(x2＋y2＋z2)≥(x＋2y＋3z)2＝a2，即14(x2＋y2＋z2)≥a2，
∴ x2＋y2＋z2≥
，即x2＋y2＋z2的最小值为.
练习册系列答案
相关题目
某校为了研究学生的性别和对待某一活动的态度(支持和不支持的两种态度)的关系，运用2×2列联表进行独立性检验，经计算K2＝7.069，则所得到的统计学结论是：有________的把握认为“学生性别与支持该活动有关系”( )
附：
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
A.0.1% B．1%
C．99% D．99.9%
＝1(a＞b＞0)，F1(－c,0)，F2(c,0)为椭圆的两个焦点，M为椭圆上任意一点，且|MF1|，|F1F2|，|MF2|构成等差数列，点F2(c,0)到直线l：x＝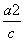
的距离为3.
，求出该圆的方程．
，求x＋y＋z的值．
对应的变换作用下得到的图形．
化为普通方程，并说明它表示的图形．