Question

已知椭圆E：＝1(a＞b＞0)，F₁(－c,0)，F₂(c,0)为椭圆的两个焦点，M为椭圆上任意一点，且|MF₁|，|F₁F₂|，|MF₂|构成等差数列，点F₂(c,0)到直线l：x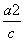＝的距离为3.

(1)求椭圆E的方程；

(2)若存在以原点为圆心的圆，使该圆的任意一条切线与椭圆E恒有两个交点A，B，且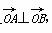，求出该圆的方程．

Answer 1

解析：　(1)由题知2|F₁F₂|＝|MF₁|＋|MF₂|，

即2×2c＝2a，得a＝2c.

又由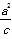－c＝3，解得c＝1，a＝2，b＝.

∴椭圆E的方程为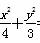＝1.

(2)假设以原点为圆心，r为半径的圆满足条件．

(ⅰ)若圆的切线的斜率存在，并设其方程为y＝kx＋m，则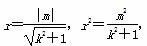，①

由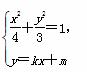消去y，整理得(3＋4k²)x²＋8kmx＋4(m²－3)＝0，设A(x₁，y₁)，B(x₂，y₂)，有

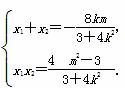
又∵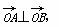∴x₁x₂＋y₁y₂＝0，

即4(1＋k²)(m²－3)－8k²m²＋3m²＋4k²m²＝0，化简得m²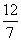＝(k²＋1)，②

由①②求得r²＝.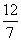

所求圆的方程为x²＋y²＝.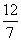

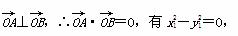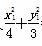(ⅱ)若AB的斜率不存在，设A(x₁，y₁)，则B(x₁，－y₁)，∵x＝y，代入＝1，得x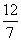＝.此时仍有r²＝＝.

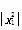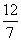综上，总存在以原点为圆心的圆x²＋y²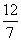＝满足题设条件．