题目内容
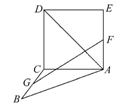
如图,在直三棱柱
 中,
中,
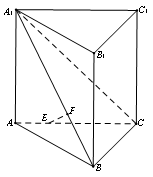 平面
平面
 侧面
侧面
 ,
,
 ,
,

 ,
,
且满足
 .
.
(1)求证:
 ;
;
(2)求二面角
 的平面角的余弦值.
的平面角的余弦值.
解:(1)证明:如右图,过 作
作 ,垂足为
,垂足为 ,
,
因平面 侧面
侧面 , 且
, 且
 平面
平面 侧面
侧面
 ,
,
可知 ,有
,有 ,
,
又 ,
, ,则
,则 ,
,
又

 平面
平面 ,所以
,所以 .因为三棱柱ABC—A1B1C1是直三棱柱,则
.因为三棱柱ABC—A1B1C1是直三棱柱,则
 底面
底面 ,所以
,所以 .又
.又


 ,从而
,从而
 侧面
侧面 ,又
,又

 侧面
侧面 ,故
,故
 . (6分)
. (6分)
(2)设平面  的法向量为
的法向量为 ,易知平面
,易知平面  的法向量可以为
的法向量可以为 .由
.由
 ,令
,令 ,则
,则 ,可得平面
,可得平面  的一个法向量可为
的一个法向量可为 ,设
,设 与
与 的夹角为
的夹角为 .则
.则 ,易知二面角
,易知二面角
 的平面角为钝角,故应为角
的平面角为钝角,故应为角 的补角,所以其余弦值为
的补角,所以其余弦值为 .(12分)
.(12分)

练习册系列答案
相关题目
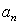 }中,
}中,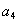 =14,前10项和
=14,前10项和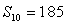 .
.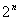 项按原来的顺序排成一个新数列{
项按原来的顺序排成一个新数列{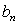 },
},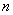 项和
项和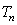 .
. .
. 

 是虚数单位,
是虚数单位, ,在复平面内,复数
,在复平面内,复数 对应的点位于( )
对应的点位于( ) ,若存在区间
,若存在区间 ,使得
,使得 ,则称函数
,则称函数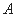 为函数
为函数 (B)
(B)
 (D)
(D)
 不论
不论 为何值时,其图像恒过的定点为
为何值时,其图像恒过的定点为 外接圆的圆心为O,AB=2,AC=3,BC=
外接圆的圆心为O,AB=2,AC=3,BC= ,则
,则 ·
· =________.
=________.