题目内容
证明不等式：a，b，c∈R，a4＋b4＋c4≥abc(a＋b＋c)．
证明 ∵a4＋b4≥2a2b2，b4＋c4≥2b2c2，
c4＋a4≥2c2a2，
∴2(a4＋b4＋c4)≥2(a2b2＋b2c2＋c2a2)
即a4＋b4＋c4≥a2b2＋b2c2＋c2a2.
又a2b2＋b2c2≥2ab2c，b2c2＋c2a2≥2abc2，
c2a2＋a2b2≥2a2bc.
∴2(a2b2＋b2c2＋c2a2)≥2(ab2c＋abc2＋a2bc)，
即a2b2＋b2c2＋c2a2≥abc(a＋b＋c)．
∴a4＋b4＋c4≥abc(a＋b＋c)．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
≥2的解为( )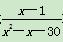
>0的解集是
ln x，
则目标函数z＝|x＋3y|的最大值为( )
，α∈
，则
等于( )
B．－