题目内容
1.直线l1:x+my-2=0与直线l2:2x+(1-m)y+2=0平行,则m的值为$\frac{1}{3}$.分析 由2m-(1-m)=0,解得m,经过验证即可得出.
解答 解:由2m-(1-m)=0,解得m=$\frac{1}{3}$,
经过验证满足条件,因此m=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题考查了相互平行的直线斜率之间的关系,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
12.下列命题中,真命题的个数有( )
①?x∈R,x2-x+$\frac{1}{4}$≥0;
②?x>0,lnx+$\frac{1}{lnx}$≤2;
③“a>b”是“ac2>bc2”的充要条件;
④f(x)=3x-3-x是奇函数.
①?x∈R,x2-x+$\frac{1}{4}$≥0;
②?x>0,lnx+$\frac{1}{lnx}$≤2;
③“a>b”是“ac2>bc2”的充要条件;
④f(x)=3x-3-x是奇函数.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13.若点M(x,y)为平面区域$\left\{\begin{array}{l}x+y≥2\\ x≤1\\ y≤2\end{array}\right.$上的一个动点,则x-y的取值范围是( )
| A. | [-2,0] | B. | [-1,0] | C. | [-1,-2] | D. | [0,2] |
11.已知全集U=R,A={x|x2-3x-4>0},B={x|-2≤x≤2},则如图所示的阴影部分所表示的集合为( )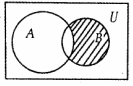

| A. | {x|-2≤x<4} | B. | {x|x≤2或x≥4} | C. | {x|-2≤x≤-1} | D. | {x|-1≤x≤2} |