题目内容
已知函数f(x)=x,数列{an}满足an=f(n+1)(n∈N+)
(Ⅰ)求数列{
}的前n项和Sn;
(Ⅱ)关于x的不等式mx2-1≥f(x)(x<0)能成立,求实数m的取值范围.
(Ⅰ)求数列{
| 1 |
| anan+1 |
(Ⅱ)关于x的不等式mx2-1≥f(x)(x<0)能成立,求实数m的取值范围.
考点:数列的求和,数列递推式
专题:函数的性质及应用,等差数列与等比数列
分析:(Ⅰ)由已知条件结合函数表达式,得
=
=
-
,由此利用裂项求和法能求出数列{
}的前n项和.
(Ⅱ)原题等价于mx2-x-1≥0在(-∞,0)内有解,由此利用m=0、m>0、m<0三种情况进行分类讨论,结合一元二次不等式的解的情况能求出实数m的取值范围.
| 1 |
| anan+1 |
| 1 |
| (n+1)(n+2) |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| anan+1 |
(Ⅱ)原题等价于mx2-x-1≥0在(-∞,0)内有解,由此利用m=0、m>0、m<0三种情况进行分类讨论,结合一元二次不等式的解的情况能求出实数m的取值范围.
解答:
解:(Ⅰ)∵函数f(x)=x,数列{an}满足an=f(n+1)(n∈N+),
∴an=n+1,
∴
=
=
-
,
∴数列{
}的前n项和:
Sn=
-
+
-
+…+
-
=
-
=
.
(Ⅱ)∵关于x的不等式mx2-1≥f(x)(x<0)能成立,
∴mx2-x-1≥0在(-∞,0)内有解,
当m=0时,-x-1≥0,解得x≤-1,成立;
当m>0时,解方程mx2-x-1=0,得x1=
,x2=
,
∴mx2-x-1≥0的解集为x≥
或x≤
,成立;
当m<0时,由△=1+4m>0,得-
<m<0,
解方程mx2-x-1=0,得x1=
>0,x2=
>0,
∴mx2-x-1≥0的解集为
<x<
,在x<0内无解,不成立.
综上,实数m的取值范围是{m|m≥0}.
∴an=n+1,
∴
| 1 |
| anan+1 |
| 1 |
| (n+1)(n+2) |
| 1 |
| n+1 |
| 1 |
| n+2 |
∴数列{
| 1 |
| anan+1 |
Sn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2 |
| 1 |
| n+2 |
| n |
| 2n+4 |
(Ⅱ)∵关于x的不等式mx2-1≥f(x)(x<0)能成立,
∴mx2-x-1≥0在(-∞,0)内有解,
当m=0时,-x-1≥0,解得x≤-1,成立;
当m>0时,解方程mx2-x-1=0,得x1=
1-
| ||
| 2m |
1+
| ||
| 2 |
∴mx2-x-1≥0的解集为x≥
1+
| ||
| 2m |
1-
| ||
| 2m |
当m<0时,由△=1+4m>0,得-
| 1 |
| 4 |
解方程mx2-x-1=0,得x1=
1-
| ||
| 2m |
1+
| ||
| 2 |
∴mx2-x-1≥0的解集为
1-
| ||
| 2m |
1+
| ||
| 2 |
综上,实数m的取值范围是{m|m≥0}.
点评:本题考查数列的前n项和的求法,考查实数的取值范围的求法,解题时要认真审题,注意裂基求和法和一元二次不等式的性质的合理运用.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
气象台预报“厦门市明天降雨的概率是80%”,下列理解正确的是( )
| A、厦门市明天将有80%的地区降雨 |
| B、厦门市明天将有80%的时间降雨 |
| C、明天出行不带雨具肯定要淋雨 |
| D、明天出行不带雨具淋雨的可能性很大 |
在一次篮球投篮比赛中,甲、乙两名球员各投篮一次,设命题p:“甲球员投篮命中”,q:“乙球员投篮命中”,则命题“至少有一名球员没有投中”可表示为( )
| A、p∨q |
| B、p∨(¬q) |
| C、(¬p)∧(¬q) |
| D、(¬p)∨(¬q) |
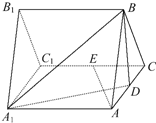 如图,三棱柱ABC-A1B1C1的所有棱长都是2,又AA1⊥平面ABC,D,E分别是AC,CC1的中点.
如图,三棱柱ABC-A1B1C1的所有棱长都是2,又AA1⊥平面ABC,D,E分别是AC,CC1的中点.