题目内容
已知arccos（2x-1）=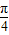
，则x的值 ．
【答案】分析：利用反余弦函数y=arccosx的性质cos[arccos（2x-1）]=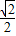
即可求得答案．
解答：解：∵arccos（2x-1）=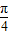
，
∴cos[arccos（2x-1）]=2x-1=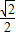
，
∴x=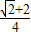
．
故答案为：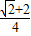
．
点评：本题考查反三角函数的运用，掌握反余弦函数的性质是关键，属于中档题．
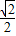即可求得答案．解答：解：∵arccos（2x-1）=
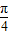，∴cos[arccos（2x-1）]=2x-1=
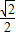，∴x=
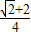．故答案为：
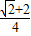．点评：本题考查反三角函数的运用，掌握反余弦函数的性质是关键，属于中档题．
练习册系列答案
相关题目
已知三点A（2，3），B（-1，-1），C（6，k），其中k为常数．若|
|=|
|，则
与
的夹角为（ ）
| AB |
| AC |
| AB |
| AC |
A、arccos(-
| ||||
B、
| ||||
C、arccos
| ||||
D、
|
已知A（3，1），B（6，1），C（4，3），D为线段BC的中点，则向量
与
的夹角为（ ）
| AC |
| DA |
A、
| ||||
B、arccos
| ||||
C、arccos（-
| ||||
D、-arccos（-
|