题目内容
已知α为锐角,且tanα=
-1,函数f(x)=2xtan2α+sin(2α+
),数列{an}的首项a1=1,an+1=f(an).
(1)求函数f(x)的表达式;
(2)若数列{bn}满足b1=a1,bn=log2(an+1),设Tn=
+
+…+
,若Tn>m对x≥2恒成立,求实数m的取值范围.
| 2 |
| π |
| 4 |
(1)求函数f(x)的表达式;
(2)若数列{bn}满足b1=a1,bn=log2(an+1),设Tn=
| 1 |
| b1+n |
| 1 |
| b2+n |
| 1 |
| bn+n |
考点:数列与三角函数的综合
专题:计算题,等差数列与等比数列,三角函数的求值
分析:(1)由α为锐角,且tanα=
-1可求得tan2a=
=1,2a=
,从而求出函数f(x)的表达式;
(2)由题意,an+1+1=2(an+1),则数列{an+1}的首项为2,公比为2的等比数列,从而求出bn=log2(an+1)=n,判断Tn的单调性求最小值即可.
| 2 |
| 2tanα |
| 1-tan2α |
| π |
| 4 |
(2)由题意,an+1+1=2(an+1),则数列{an+1}的首项为2,公比为2的等比数列,从而求出bn=log2(an+1)=n,判断Tn的单调性求最小值即可.
解答:
解:(1)∵tanα=
-1,
∴tan2a=
=1,
又∵α为锐角,
∴2a=
,
∴sin(2α+
)=sin
=1,
∴f(x)=2x+1;
(2)∵an+1=f(an)=2an+1,
∴an+1+1=2(an+1),
又∵a1=1,
∴数列{an+1}的首项为2,公比为2的等比数列,
∴an+1=2n,
∴bn=log2(an+1)=log22n=n,
∴Tn=
+
+…+
=
+
+…+
,
而Tn+1-Tn=
+
-
>0,
所以n≥2时,T2取得最小值,
则若Tn>m对n≥2恒成立可化为
T2>m,又∵T2=
,
则m<
.
| 2 |
∴tan2a=
| 2tanα |
| 1-tan2α |
又∵α为锐角,
∴2a=
| π |
| 4 |
∴sin(2α+
| π |
| 4 |
| π |
| 2 |
∴f(x)=2x+1;
(2)∵an+1=f(an)=2an+1,
∴an+1+1=2(an+1),
又∵a1=1,
∴数列{an+1}的首项为2,公比为2的等比数列,
∴an+1=2n,
∴bn=log2(an+1)=log22n=n,
∴Tn=
| 1 |
| b1+n |
| 1 |
| b2+n |
| 1 |
| bn+n |
| 1 |
| 1+n |
| 1 |
| 2+n |
| 1 |
| 2n |
而Tn+1-Tn=
| 1 |
| 2n+1 |
| 1 |
| 2n+2 |
| 1 |
| n+1 |
所以n≥2时,T2取得最小值,
则若Tn>m对n≥2恒成立可化为
T2>m,又∵T2=
| 7 |
| 12 |
则m<
| 7 |
| 12 |
点评:本题考查了三角函数的求值及等差数列与等比数列的化简与求值,同时考查了数列的单调性的判断,属于中档题.

练习册系列答案
相关题目
已知圆(x-3)2+(y-4)2=4和直线y=x相交于P,Q两点则|OP|•|OQ|的值是( )
A、
| ||
| B、2 | ||
| C、4 | ||
| D、21 |
函数f(x)=x3-3x2-9x+3,若函数g(x)=f(x)-m,在x∈[-2,5]上有3个零点,则m的取值范围为( )
| A、[1,8] |
| B、(-24,1] |
| C、[1,8) |
| D、(-24,8) |
如图,在长方形ABCD中,AB=
,BC=1,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )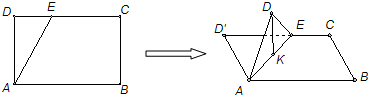
| 3 |

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
数列1,3,6,10…的一个通项公式是( )
| A、an=n2-(n-1) | ||
B、an=
| ||
| C、an=n2-1 | ||
D、an=
|
下列命题正确的是( )
| A、若a>b,则ac2>bc2 | ||||
| B、若a2>b2,则a>b | ||||
C、若
| ||||
D、若
|
