题目内容
设椭圆与双曲线有共同的焦点F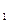 (-4,0)、F
(-4,0)、F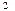 (4,0),并且椭圆和长轴长是双曲线实轴长的2倍,试求椭圆与双曲线交点的轨迹方程。
(4,0),并且椭圆和长轴长是双曲线实轴长的2倍,试求椭圆与双曲线交点的轨迹方程。
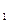 (-4,0)、F
(-4,0)、F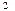 (4,0),并且椭圆和长轴长是双曲线实轴长的2倍,试求椭圆与双曲线交点的轨迹方程。
(4,0),并且椭圆和长轴长是双曲线实轴长的2倍,试求椭圆与双曲线交点的轨迹方程。所求轨迹方程是(x-5)  +y
+y =9(y≠0)或(x+5)
=9(y≠0)或(x+5)  +y
+y =9(y≠0)。
=9(y≠0)。
 +y
+y =9(y≠0)或(x+5)
=9(y≠0)或(x+5)  +y
+y =9(y≠0)。
=9(y≠0)。设椭圆与双曲线的交点为P(x,y)(y≠0),由椭圆与双曲线的定义及条件,可得|PF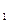 |+|P F
|+|P F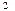 |=
|=
| |p F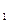 |-|p F
|-|p F | |,即|PF
| |,即|PF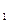 |="3|P" F
|="3|P" F |,或|P F
|,或|P F |=3|PF
|=3|PF |。将P、F
|。将P、F 、F
、F 的坐标代入,并化简,得(x-5)
的坐标代入,并化简,得(x-5)  +y
+y =9或(x+5)
=9或(x+5)  +y
+y =9,且y≠0。
=9,且y≠0。
∴所求轨迹方程是(x-5) +y
+y =9(y≠0)或(x+5)
=9(y≠0)或(x+5)  +y
+y =9(y≠0)。
=9(y≠0)。
 |+|P F
|+|P F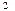 |=
|=| |p F
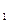 |-|p F
|-|p F | |,即|PF
| |,即|PF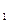 |="3|P" F
|="3|P" F |,或|P F
|,或|P F |=3|PF
|=3|PF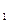 |。将P、F
|。将P、F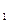 、F
、F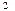 的坐标代入,并化简,得(x-5)
的坐标代入,并化简,得(x-5)  +y
+y =9或(x+5)
=9或(x+5)  +y
+y =9,且y≠0。
=9,且y≠0。∴所求轨迹方程是(x-5)
 +y
+y =9(y≠0)或(x+5)
=9(y≠0)或(x+5)  +y
+y =9(y≠0)。
=9(y≠0)。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 过定点
过定点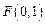 ,且和定直线
,且和定直线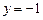 相切.(Ⅰ)求动圆圆心
相切.(Ⅰ)求动圆圆心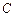 的方程;(Ⅱ)已知点
的方程;(Ⅱ)已知点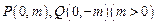 ,过点
,过点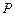 作直线与曲线
作直线与曲线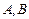 两点,若
两点,若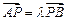 (
(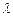
 为实数),证明:
为实数),证明: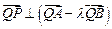 .
.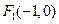 出发,经直线l:
出发,经直线l: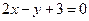 上一点
上一点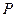 反射后,恰好穿过点
反射后,恰好穿过点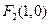 .(1)求
.(1)求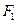 、
、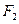 为焦点且过点
为焦点且过点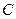 的方程; (3)设点
的方程; (3)设点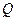 是椭圆
是椭圆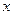 轴上是否存在两定点
轴上是否存在两定点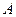 、
、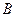 ,使得直线
,使得直线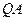 、
、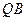 的斜率之积为定值?若存在,请求出定值,并求出所有满足条件的定点
的斜率之积为定值?若存在,请求出定值,并求出所有满足条件的定点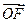 所在直线为
所在直线为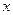 轴,建立如 所示的坐标系。设
轴,建立如 所示的坐标系。设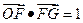 ,点F的坐标为
,点F的坐标为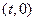 ,
,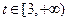 ,点G的坐标为
,点G的坐标为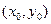 。
。 关于
关于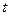 的函数
的函数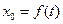 的表达式,判断函数
的表达式,判断函数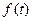 的单调性,并证明你的判断;
的单调性,并证明你的判断;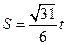 ,若以O为中心,F为焦点的椭圆经过点G,求当
,若以O为中心,F为焦点的椭圆经过点G,求当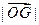 取最小值时椭圆的方程;
取最小值时椭圆的方程;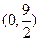 ,C、D是椭圆上的两点,且
,C、D是椭圆上的两点,且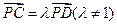 ,求实数
,求实数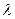 的取值范围。
的取值范围。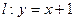 与曲线
与曲线
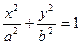
 交于不同的两点
交于不同的两点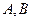 ,
,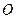 为坐标原点.
为坐标原点.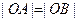 ,求证:曲线
,求证:曲线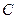 是一个圆;
是一个圆; ,当
,当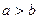 且
且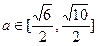 时,求曲线
时,求曲线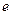 的取值范围.
的取值范围.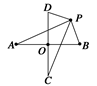
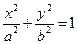 (a>b>0)的左顶点为A,若椭圆上存在一点P,使∠OPA=
(a>b>0)的左顶点为A,若椭圆上存在一点P,使∠OPA=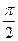 (O为原点),求椭圆离心率的取值范围.
(O为原点),求椭圆离心率的取值范围.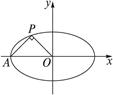
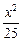 +
+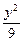 =1上一点P到左焦点F1的距离为2,M是线段PF1的中点,则M到原点O的距离等于
=1上一点P到左焦点F1的距离为2,M是线段PF1的中点,则M到原点O的距离等于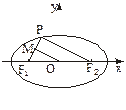
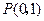 且与抛物线
且与抛物线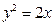 只有一个公共点的直线的方程.
只有一个公共点的直线的方程.