题目内容
设椭圆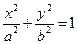 (a>b>0)的左顶点为A,若椭圆上存在一点P,使∠OPA=
(a>b>0)的左顶点为A,若椭圆上存在一点P,使∠OPA=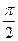 (O为原点),求椭圆离心率的取值范围.
(O为原点),求椭圆离心率的取值范围.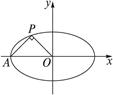
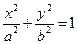 (a>b>0)的左顶点为A,若椭圆上存在一点P,使∠OPA=
(a>b>0)的左顶点为A,若椭圆上存在一点P,使∠OPA=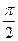 (O为原点),求椭圆离心率的取值范围.
(O为原点),求椭圆离心率的取值范围.
椭圆离心率的范围是( ,1).
,1).
 ,1).
,1).如图,设P(x,y),由∠OPA=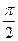 知点P在以AO为直径的圆上,
知点P在以AO为直径的圆上,
即 .
.
联立方程组 消去y,得
消去y,得
(a2-b2)x2+a3x+a2b2=0.
解之,得x=-a或 .
.
当x=-a时,P与A重合,不满足题意,舍去.
故P点的横坐标为 .
.
又∵ ,∴a2>2b2,即a2>2(a2-c2).
,∴a2>2b2,即a2>2(a2-c2).
∴ ,
, .
.
又∵0<e<1,
∴ 1,即椭圆离心率的范围是(
1,即椭圆离心率的范围是( ,1).
,1).
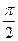 知点P在以AO为直径的圆上,
知点P在以AO为直径的圆上,即
 .
.联立方程组
 消去y,得
消去y,得(a2-b2)x2+a3x+a2b2=0.
解之,得x=-a或
 .
.当x=-a时,P与A重合,不满足题意,舍去.
故P点的横坐标为
 .
.又∵
 ,∴a2>2b2,即a2>2(a2-c2).
,∴a2>2b2,即a2>2(a2-c2).∴
 ,
, .
.又∵0<e<1,
∴
 1,即椭圆离心率的范围是(
1,即椭圆离心率的范围是( ,1).
,1).
练习册系列答案
相关题目
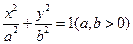 的焦点坐
的焦点坐 标为
标为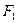 (
(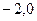 ),点M(
),点M(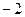 ,
,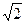 )在椭圆E上
)在椭圆E上 (1)求椭圆E的方程;(2)O为坐标原点,⊙
(1)求椭圆E的方程;(2)O为坐标原点,⊙ 的任意一条切线与椭圆E有两个交点
的任意一条切线与椭圆E有两个交点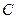 ,
,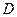 且
且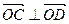 ,求⊙
,求⊙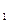 (-4,0)、F
(-4,0)、F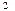 (4,0),并且椭圆和长轴长是双曲线实轴长的2倍,试求椭圆与双曲线交点的轨迹方程。
(4,0),并且椭圆和长轴长是双曲线实轴长的2倍,试求椭圆与双曲线交点的轨迹方程。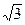 ≈1.7,
≈1.7,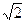 ≈1.4)( )
≈1.4)( )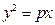 和圆
和圆 ,它们在
,它们在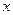 轴上方的交点为
轴上方的交点为 ,那么当
,那么当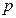 为何值时,线段
为何值时,线段 的中点
的中点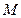 在直线
在直线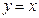 上?
上?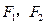 是椭圆的两个焦点,
是椭圆的两个焦点,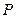 为椭圆上一点,
为椭圆上一点,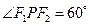 .
.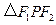 的面积只与椭圆的短轴长有关.
的面积只与椭圆的短轴长有关.