题目内容
4.已知函数f(x)是定义在R上的偶函数,f(2)=0,x>0时,$\frac{xf′(x)-f(x)}{{x}^{2}}$<0,则不等式xf(x)<0的解集(-2,0)∪(2,+∞).分析 令g(x)=$\frac{f(x)}{x}$,根据函数的单调性和函数的奇偶性求出不等式的解集即可.
解答 解:令g(x)=$\frac{f(x)}{x}$,
∵x>0时,g′(x)=$\frac{xf′(x)-f(x)}{{x}^{2}}$<0,
∴g(x)在(0,+∞)递减,
∵f(-x)=f(x),
∴g(-x)=$\frac{f(-x)}{-x}$=-g(x),
g(x)在(-∞,0)递减,
∴g(x)是奇函数,
g(2)=$\frac{f(2)}{2}$=0,
∴0<x<2时,g(x)>0,x>2时,g(x)<0,
根据函数的奇偶性,-2<x<0时,g(x)<0,x<-2时,g(x)>0,
xf(x)<0,即x2g(x)<0,即g(x)<0,
∴x>2或-2<x<0,
故答案为:(-2,0)∪(2,+∞).
点评 本题主要考察函数奇偶性的应用,考查函数的单调性,是一道中档题.

练习册系列答案
相关题目
16.在△ABC中,边AC长为$\sqrt{5}$,|${\overrightarrow{CA}$+$\overrightarrow{CB}}$|=2$\sqrt{5}$,D是BC边上的点,且$\overrightarrow{BD}$=2$\overrightarrow{DC}$,$\overrightarrow{AD}$•$\overrightarrow{BC}$=0,则cos∠BAC=( )
| A. | $\frac{{\sqrt{5}}}{10}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{10}}}{5}$ | D. | $\frac{{\sqrt{10}}}{10}$ |
13.已知函数f(x)=x2+(a+8)x+a2+a-12(a<0),且f(a2-4)=f(2a-8),则$\frac{f(n)-4a}{n+1}(n∈{N^+})$的最小值为( )
| A. | $\frac{37}{4}$ | B. | $\frac{35}{8}$ | C. | $\frac{28}{3}$ | D. | $\frac{27}{4}$ |
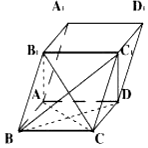 如图,斜四棱柱ABCD-A1B1C1D1的底面是边长为$\sqrt{3}$的正方形,侧面A1ABB1⊥底面ABCD,AA1=2,∠B1BA=30°.
如图,斜四棱柱ABCD-A1B1C1D1的底面是边长为$\sqrt{3}$的正方形,侧面A1ABB1⊥底面ABCD,AA1=2,∠B1BA=30°.