题目内容
1.在△ABC中,A=60°,2asinB=3,则b=$\sqrt{3}$.分析 由正弦定理可得b=$\frac{asinB}{sinA}$,整体代入计算可得.
解答 解:由正弦定理可得$\frac{b}{sinB}$=$\frac{a}{sinA}$,
∴b=$\frac{asinB}{sinA}$=$\frac{3}{2×\frac{\sqrt{3}}{2}}$=$\sqrt{3}$
故答案为:$\sqrt{3}$
点评 本题考查正弦定理解三角形,属基础题.

练习册系列答案
相关题目
14.函数f(x)在x=x0处导数存在,若p:f′(x0)=0;q:x=x0是f(x)的极值点,则p是q的( )
| A. | 充分不必要条件 | B. | 充要条件 | ||
| C. | 必要不充条件 | D. | 既非充分条件也非必要条件 |
6.已知集合M={x|$\frac{x-3}{x+1}$<0},N={x|x≤-1},则集合{x|x≥3}等于( )
| A. | M∩N | B. | M∪N | C. | ∁R(M∩N) | D. | ∁R(M∪N) |
13.与向量$\overrightarrow{a}$=(3,4)共线反向的单位向量$\overrightarrow{e}$=( )
| A. | (-$\frac{3}{5}$,-$\frac{4}{5}$) | B. | (-$\frac{4}{5}$,$\frac{3}{5}$) | C. | (-$\frac{3}{5}$,-$\frac{4}{5}$),($\frac{3}{5}$,$\frac{4}{5}$) | D. | ($±\frac{3}{5}$,$±\frac{4}{5}$) |
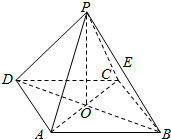 已知:正四棱锥P-ABCD,O为正方形ABCD的中心,PA与底ABCD所成的角为α,且cosα=$\frac{\sqrt{10}}{5}$.
已知:正四棱锥P-ABCD,O为正方形ABCD的中心,PA与底ABCD所成的角为α,且cosα=$\frac{\sqrt{10}}{5}$.