题目内容
数列{an}中,前n项和Sn=n2an且a1=1,则an= .
考点:数列的函数特性
专题:等差数列与等比数列
分析:当n≥2时,an=Sn-Sn-1=n2an-(n-1)2an-1,可得
=
.利用an=
•
•…•
•a1即可得出.
| an |
| an-1 |
| n-1 |
| n+1 |
| an |
| an-1 |
| an-1 |
| an-2 |
| a2 |
| a1 |
解答:
解:当n≥2时,an=Sn-Sn-1=n2an-(n-1)2an-1,
化为
=
.
∴an=
•
•…•
•a1
=
•
•
•…•
×
×1=
.
∴an=
.
故答案为:
.
化为
| an |
| an-1 |
| n-1 |
| n+1 |
∴an=
| an |
| an-1 |
| an-1 |
| an-2 |
| a2 |
| a1 |
=
| n-1 |
| n+1 |
| n-2 |
| n |
| n-3 |
| n-1 |
| 2 |
| 4 |
| 1 |
| 3 |
| 2 |
| n(n+1) |
∴an=
| 2 |
| n(n+1) |
故答案为:
| 2 |
| n(n+1) |
点评:本题考查了利用“当n≥2时,an=Sn-Sn-1”和“累乘求积”求数列的通项公式的方法,考查了推理能力和计算能力,属于中档题.

练习册系列答案
相关题目
函数f(x)=x2-3x+2的零点是( )
| A、(1,0),(2,0) |
| B、(0,1),(0,2) |
| C、1,2 |
| D、-1,-2 |
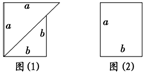 如图所示的两种广告牌,其中图(1)是由两个等腰直角三角形构成的,图(2)是一个矩形,则这两个广告牌面积的大小关系可用含字母a,b(a≠b)的不等式表示为
如图所示的两种广告牌,其中图(1)是由两个等腰直角三角形构成的,图(2)是一个矩形,则这两个广告牌面积的大小关系可用含字母a,b(a≠b)的不等式表示为