题目内容
已知点O在△ABC内部，且| OA |
| OB |
| OC |
| 0 |
分析：由向量式可得O为三角形ABC中位线DE的三等分点（靠近D），从而可得两三角形面积和△ABC的关系，可从而得答案．
解答：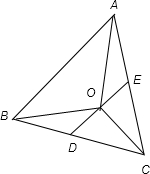
解：∵
+2
+3
=
，∴
+
+2（
+
）=
，
如图D，E分别是对应边的中点，
由平行四边形法则知
+
=2
，
+
=2
，
∴
=-2
，∴O为三角形ABC中位线DE的三等分点（靠近D）
∴O到AB的距离是三角形ABC高的一半，O到BC的距离是三角形ABC高的
，
∴S△OAB=
S△ABC，S△OBC=
S△ABC
∴△OAC的面积与△OAB的面积之比为 3：1
故答案为：3：1
解：∵| OA |
| OB |
| OC |
| 0 |
| OA |
| OC |
| OB |
| OC |
| 0 |
如图D，E分别是对应边的中点，
由平行四边形法则知
| OA |
| OC |
| OE |
| OB |
| OC |
| OD |
∴
| OE |
| OD |
∴O到AB的距离是三角形ABC高的一半，O到BC的距离是三角形ABC高的
| 1 |
| 6 |
∴S△OAB=
| 1 |
| 2 |
| 1 |
| 6 |
∴△OAC的面积与△OAB的面积之比为 3：1
故答案为：3：1
点评：本题考查向量的线性运算和三角形的面积公式，由向量式得出O的位置是解决问题的关键，属中档题．
练习册系列答案
相关题目
，向△ABC内任抛一点M，则点M落在△AOB内的概率为________．
，向△ABC内任抛一点M，则点M落在△AOB内的概率为 ．
，向△ABC内任抛一点M，则点M落在△AOC内的概率为 。