题目内容
9.已知满足$\left\{\begin{array}{l}{x+y-3≤0}\\{2x-y≥0}\end{array}\right.$的点P(x,y)不在函数y=ax的图象上,则实数a的取值范围为(2,+∞).分析 根据已知的约束条件 画出满足约束条件的可行域,再用图象判断,求出目标函数的最小值
解答  解:由$\left\{\begin{array}{l}{x+y-3≤0}\\{2x-y≥0}\end{array}\right.$画出满足条件的可行域,
解:由$\left\{\begin{array}{l}{x+y-3≤0}\\{2x-y≥0}\end{array}\right.$画出满足条件的可行域,
由$\left\{\begin{array}{l}{x+y-3=0}\\{2x-y=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$,得到点A(1,2),
当A(1,2)在函数y=ax的图象上,
此时2=a,
由于点P(x,y)不在函数y=ax的图象上,
所以实数a的取值范围为(2,+∞).
点评 本题考查的知识点是线性规划,处理的思路为:借助于平面区域特性,用几何方法处理代数问题,体现了数形结合思想、化归思想.

练习册系列答案
相关题目
20.函数f(x)的图象向左平移一个单位长度,所得的图象与函数y=2x的图象关于y轴对称,则f(x)=( )
| A. | y=2x-1 | B. | y=${(\frac{1}{2})^{x-1}}$ | C. | y=${(\frac{1}{2})^{x+1}}$ | D. | y=2x+1 |
1.若x+y=1,则sinx+siny与1的大小关系是( )
| A. | sinx+siny>1 | B. | sinx+siny=1 | C. | sinx+siny<1 | D. | 随x、y的值而定 |
18.设△ABC中的内角A,B,C所对的边长分别为a,b,c,且asinB=2sin$\frac{A}{2}$,cos$\frac{A}{2}$=$\frac{2}{3}$,则b等于( )
| A. | 1 | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{4}{3}$ |
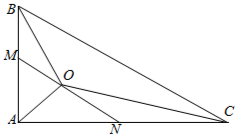 如图所示,△ABC中,AB⊥AC,AB=6,AC=8.边AB,AC的中点分别为M,N.若O为线段MN上任一点,则$\overrightarrow{OB}•\overrightarrow{OC}+\overrightarrow{OA}•\overrightarrow{OB}+\overrightarrow{OA}•\overrightarrow{OC}$的取值范围是[$-\frac{180}{11},-9$].
如图所示,△ABC中,AB⊥AC,AB=6,AC=8.边AB,AC的中点分别为M,N.若O为线段MN上任一点,则$\overrightarrow{OB}•\overrightarrow{OC}+\overrightarrow{OA}•\overrightarrow{OB}+\overrightarrow{OA}•\overrightarrow{OC}$的取值范围是[$-\frac{180}{11},-9$].