题目内容
【题目】对于数列{an},定义 ![]() 为{an}的“优值”,现在已知某数列{an}的“优值”
为{an}的“优值”,现在已知某数列{an}的“优值” ![]() ,记数列{an﹣kn}的前n项和为Sn , 若Sn≤S5对任意的n∈N+恒成立,则实数k的最大值为 .
,记数列{an﹣kn}的前n项和为Sn , 若Sn≤S5对任意的n∈N+恒成立,则实数k的最大值为 .
【答案】![]()
【解析】解:由题意, ![]() =2n+1 , 则a1+2a2+…+2n﹣1an=n2n+1 ,
=2n+1 , 则a1+2a2+…+2n﹣1an=n2n+1 ,
当n≥2时,a1+2a2+…+2n﹣2an﹣1=(n﹣1)2n ,
两式相减可得2n﹣1an=n2n+1﹣(n﹣1)2n=(n+1)2n ,
则an=2(n+1),
当n=1时,a1=4,
上式对a1也成立,
故an=2(n+1),n∈N+ ,
则an﹣kn=(2﹣k)n+2,
则数列{an﹣kn}为等差数列,
故Sn≤S5对任意的n(n∈N*)恒成立可化为
a5≥0,a6≤0,
即 ![]() ,
,
解得 ![]() ≤k≤
≤k≤ ![]() ,
,
则实数k的最大值为 ![]() ,
,
所以答案是: ![]() .
.
【考点精析】本题主要考查了数列的前n项和的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系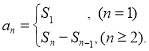 才能正确解答此题.
才能正确解答此题.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目