题目内容
【题目】已知点A,B,C的坐标分别为A(3,0),B(0,3),C(cos α,sin α),α∈![]() .
.
(1)若|![]() |=|
|=|![]() |,求角α的值;
|,求角α的值;
(2)若![]() =-1,求
=-1,求![]() 的值.
的值.
【答案】(1)α=![]() ;(2)-
;(2)-![]() .
.
【解析】试题分析:(1)根据两向量的模相等,利用两点间的距离公式建立等式求得tanα的值,根据α的范围求得α.
(2)根据向量的基本运算根据![]() =-1,求得sin
=-1,求得sin ![]() +cos
+cos ![]() =
=![]() ,然后同角和与差的关系可得到2sin
,然后同角和与差的关系可得到2sin ![]() cos
cos ![]() =-
=-![]() ,化简代入即可.
,化简代入即可.
试题解析:
(1)∵![]() =(cos
=(cos ![]() -3,sin
-3,sin ![]() ),
),![]() =(cos
=(cos ![]() ,sin
,sin ![]() -3),
-3),
∴|![]() |=
|=![]() ,
,
|![]() |=
|=![]() .
.
由|![]() |=|
|=|![]() |,得sin
|,得sin ![]() =cos
=cos ![]() .
.
又∵![]() ∈
∈![]() ,∴
,∴![]() =
=![]() .
.
(2)由![]() =-1,得(cos
=-1,得(cos ![]() -3)cos
-3)cos ![]() +sin
+sin ![]() (sin
(sin ![]() -3)=-1.
-3)=-1.
∴sin ![]() +cos
+cos ![]() =
=![]() . ①
. ①
又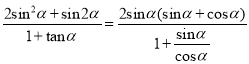 =2sin
=2sin ![]() cos
cos ![]() .
.
由①式两边平方,得1+2sin ![]() cos
cos ![]() =
=![]() ,
,
∴2sin ![]() cos
cos ![]() =-
=-![]() .
.
∴![]() =-
=-![]() .
.

练习册系列答案
相关题目