题目内容
设数列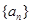 、
、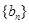 满足
满足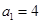 ,
,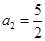 ,
,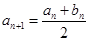 ,
,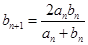 .
.
(1)证明: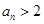 ,
,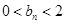 (
(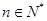 );
);
(2)设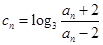 ,求数列
,求数列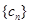 的通项公式;
的通项公式;
(3)设数列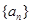 的前
的前 项和为
项和为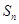 ,数列
,数列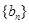 的前
的前 项和为
项和为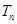 ,数列
,数列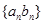 的前
的前 项和为
项和为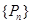 ,求证:
,求证: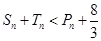 .
.
 、
、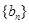 满足
满足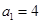 ,
,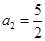 ,
,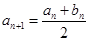 ,
,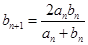 .
. (1)证明:
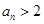 ,
,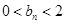 (
(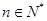 );
);(2)设
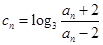 ,求数列
,求数列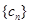 的通项公式;
的通项公式;(3)设数列
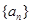 的前
的前 项和为
项和为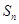 ,数列
,数列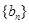 的前
的前 项和为
项和为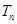 ,数列
,数列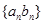 的前
的前 项和为
项和为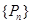 ,求证:
,求证: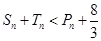 .
.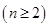
(1)
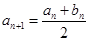 ,
,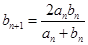 两式相乘得
两式相乘得 ,
, 为常数列,
为常数列, ;
; 

 ;
;
(2) ;(3)由
;(3)由 可以知道,
可以知道, ,
,
 .又
.又 ,故
,故 ,
,
所以
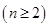 .
.

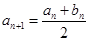 ,
,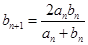 两式相乘得
两式相乘得 ,
, 为常数列,
为常数列, ;
; 

 ;
;(2)
 ;(3)由
;(3)由 可以知道,
可以知道, ,
, .又
.又 ,故
,故 ,
,所以

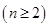 .
.试题分析:(1)

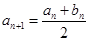 ,
,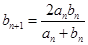 两式相乘得
两式相乘得 ,
, 为常数列,
为常数列, ;(2分)
;(2分)

 ;
;(若
 ,则
,则 ,从而可得
,从而可得 为常数列与
为常数列与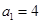 矛盾); 4分
矛盾); 4分(2)
 ,
,
又因为
 ,
, 为等比数列,
为等比数列,  8分
8分(3)由
 可以知道,
可以知道, ,
,令
 ,数列
,数列 的前
的前 项和为
项和为 ,很显然只要证明
,很显然只要证明
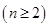 ,
, .
.因为

 ,
,



所以




所以
 . 14分
. 14分又
 ,故
,故 ,
,所以

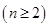 . 16分
. 16分 点评:本题考查不等式的证明和数列的通项公式的求法,综合性强,难度大,是高考重点,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 是等差数列,且
是等差数列,且 ,则数列
,则数列 项和
项和 等于
等于
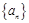 是各项均不为
是各项均不为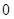 的等差数列,公差为
的等差数列,公差为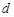 ,
,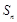 为其前
为其前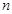 项和,且满足
项和,且满足 ,
,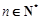 .数列
.数列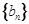 满足
满足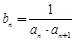 ,
,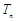 为数列
为数列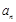 和数列
和数列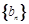 的前n项和
的前n项和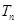 ;
;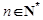 ,不等式
,不等式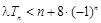 恒成立,求实数
恒成立,求实数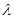 的取值范围;
的取值范围;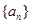 的前
的前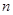 项和
项和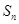 和通项
和通项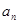 满足
满足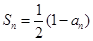 .
.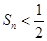 ;
;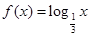 ,
,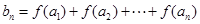 ,求
,求 .
. 中,a3+a11="8," 数列
中,a3+a11="8," 数列 是等比数列,且b7=a7,则b6b8的值为
是等比数列,且b7=a7,则b6b8的值为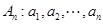 ,(例如
,(例如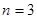 时,
时,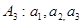 )满足
)满足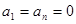 ,且当
,且当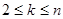 (
(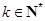 )时,
)时,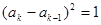 .令
.令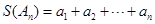 .
.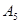 的所有可能的情况;(5分)
的所有可能的情况;(5分)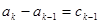 ,求
,求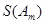 (用
(用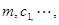
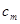 的代数式来表示);(5分)
的代数式来表示);(5分)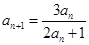 ,n=1,2,……
,n=1,2,……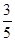 ,求
,求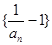 是等比数列,并求出{an}的通项公式;
是等比数列,并求出{an}的通项公式;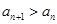 对一切
对一切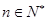 都成立,求t的取值范围.
都成立,求t的取值范围. 为等差数列,
为等差数列, ,则
,则 等于( )
等于( ) 的前
的前 项和为
项和为 ,
, ,
, ,等差数列
,等差数列 满足
满足 ,
, ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.