题目内容
(本小题满分13分)
已知数列{an}的首项a1=" t" >0,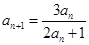 ,n=1,2,……
,n=1,2,……
(1)若t =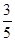 ,求
,求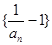 是等比数列,并求出{an}的通项公式;
是等比数列,并求出{an}的通项公式;
(2)若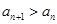 对一切
对一切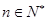 都成立,求t的取值范围.
都成立,求t的取值范围.
已知数列{an}的首项a1=" t" >0,
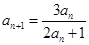 ,n=1,2,……
,n=1,2,……(1)若t =
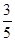 ,求
,求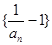 是等比数列,并求出{an}的通项公式;
是等比数列,并求出{an}的通项公式;(2)若
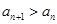 对一切
对一切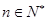 都成立,求t的取值范围.
都成立,求t的取值范围.(1)将所给关系式取导数,即得递推关系式,从而得证, (2)0<t<1
(2)0<t<1
 (2)0<t<1
(2)0<t<1试题分析:(1)由题意
 ,
, ,
,所以
 ,又因为
,又因为 , ……4分
, ……4分所以数列{
 }是首项为
}是首项为 ,公比为
,公比为 的等比数列, ……5分
的等比数列, ……5分根据等比数列的通项公式得
 ,
,所以
 . ……7分
. ……7分(2)由(1)知
 ,
, , ……9分
, ……9分由
 ,
,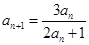 知
知 ,故由
,故由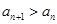 得
得 , ……10分
, ……10分即(
 -1)(
-1)( )
) +1<(
+1<( -1)(
-1)( )
) +1得
+1得 -1>0,
-1>0,又t>0,则0<t<1. ……13分
点评:由数列的递推关系式求数列的通项公式有累加法、累乘法和构造新数列法,要根据递推关系式的形式恰当选择.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
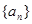 的前
的前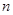 项和为
项和为 ,若
,若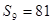 ,则
,则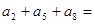
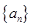 是等差数列,
是等差数列,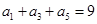 ,
,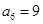 ,则这个数列的前6项和等于( )
,则这个数列的前6项和等于( )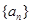 、
、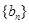 满足
满足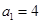 ,
,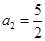 ,
,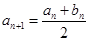 ,
,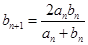 .
. 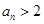 ,
,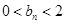 (
(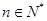 );
);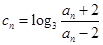 ,求数列
,求数列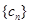 的通项公式;
的通项公式; 项和为
项和为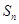 ,数列
,数列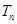 ,数列
,数列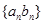 的前
的前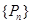 ,求证:
,求证: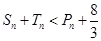 .
.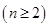
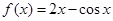 ,
,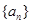 是公差为
是公差为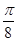 的等差数列,
的等差数列,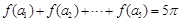 ,则
,则 .
. 满足:
满足: ,
, .
. .
. 及
及 ;
; ,
, (
( ),求数列
),求数列 的前
的前 项和
项和 .
.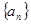 中,
中,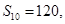 那么
那么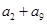 的值是( )
的值是( ) 中,
中, ,若
,若 ,则数列
,则数列 的前5项和等于 .
的前5项和等于 . 满足:
满足: ,
, ,且
,且
 ,则右图中第9行所有数的和为 ( )
,则右图中第9行所有数的和为 ( ) 