题目内容
已知数列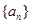 的前
的前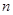 项和
项和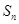 和通项
和通项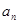 满足
满足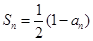 .
.
(Ⅰ)求数列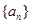 的通项公式;
的通项公式;
(Ⅱ) 求证: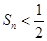 ;
;
(Ⅲ)设函数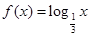 ,
,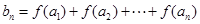 ,求
,求 .
.
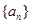 的前
的前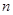 项和
项和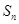 和通项
和通项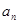 满足
满足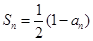 .
.(Ⅰ)求数列
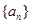 的通项公式;
的通项公式;(Ⅱ) 求证:
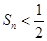 ;
;(Ⅲ)设函数
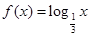 ,
,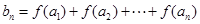 ,求
,求 .
.(Ⅰ)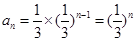 ;(Ⅱ) 由
;(Ⅱ) 由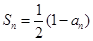 得
得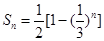

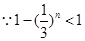 ,∴
,∴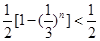 ∴
∴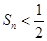 -;(Ⅲ)
-;(Ⅲ)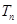 =
=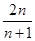
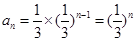 ;(Ⅱ) 由
;(Ⅱ) 由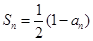 得
得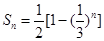

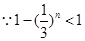 ,∴
,∴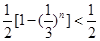 ∴
∴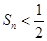 -;(Ⅲ)
-;(Ⅲ)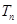 =
=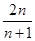
试题分析:(Ⅰ)当
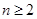 时
时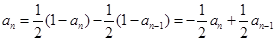 ,
,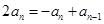
∴
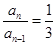 ,-------------------------------------------------3分
,-------------------------------------------------3分由
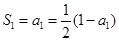 得
得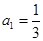
∴数列
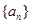 是首项
是首项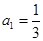 、公比为
、公比为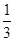 的等比数列,∴
的等比数列,∴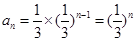 ------5分
------5分(Ⅱ)证法1: 由
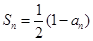 得
得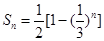
 --------------------------7分
--------------------------7分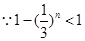 ,∴
,∴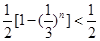 ∴
∴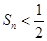 ----9分
----9分〔证法2:由(Ⅰ)知
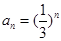 ,∴
,∴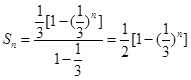 -----7分
-----7分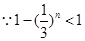 ,∴
,∴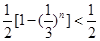 ----------------------8分
----------------------8分即
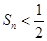 ------------------------------------9分
------------------------------------9分(Ⅲ)
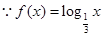
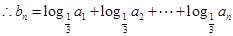 =
=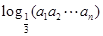 ----10分
----10分=
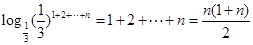 --------12分
--------12分∵
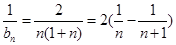
∴
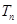
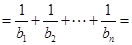
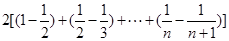 =
=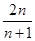 ---14分
---14分点评:对公式的变形是解决数列特征问题的关键,对于数列求和要注意针对数列的特点选择相应的求和法则

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 中,
中,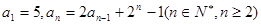 ,若存在实数
,若存在实数 ,使得数列
,使得数列 为等差数列,则
为等差数列,则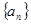 中,
中,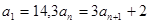 ,则使
,则使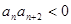 成立的
成立的 值是( )
值是( )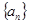 为单调递增的等差数列
为单调递增的等差数列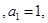 且
且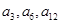 依次成等比数列.
依次成等比数列.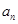 ;
;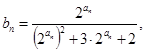 求数列
求数列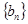 的前
的前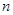 项和
项和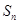 ;
;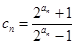 ,求证:
,求证: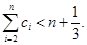
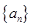 是等差数列,
是等差数列,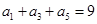 ,
,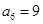 ,则这个数列的前6项和等于( )
,则这个数列的前6项和等于( )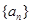 、
、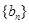 满足
满足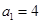 ,
,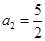 ,
,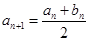 ,
,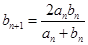 .
. 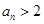 ,
,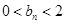 (
(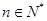 );
);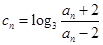 ,求数列
,求数列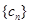 的通项公式;
的通项公式; 项和为
项和为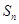 ,数列
,数列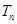 ,数列
,数列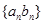 的前
的前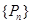 ,求证:
,求证: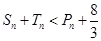 .
.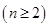
 满足:
满足: ,
, .
. .
. 及
及 ;
; ,
, (
( ),求数列
),求数列 的前
的前 项和
项和 .
. 前
前 项和为
项和为 ,
, .
. 为等比数列;
为等比数列; ,数列
,数列 前
前 ,求证:
,求证: .
.