若|x-a|+|x-a2|≥2恒成立.求a的范围．题目和参考答案——青夏教育精英家教网——

题目内容

19．若|x-a|+|x-a²|≥2（a是常数）恒成立，求a的范围．

分析由条件利用绝对值三角不等式求得|x-a|+|x-a²|≥|a²-a|，由|-a+a²|≥2，分类讨论求得a的范围．

解答解：由|x-a|+|x-a²|≥2（a是常数）恒成立，而|x-a|+|x-a²|≥|（x-a）-（x-a²）|=|-a+a²|，
∴|-a+a²|≥2，求得a²-a≥2①或 a²-a≤-2 ②．
解①求得a≥2 或a≤-1，解②求得a∈∅．
综上可得，a的范围为{a|a≥2 或a≤-1}．

点评本题主要考查绝对值三角不等式，函数的恒成立问题，属于中档题．

练习册系列答案

期末金牌卷系列答案

轻松课堂标准练系列答案

全程畅优大考卷系列答案

淘金先锋课堂系列答案

整合集训随堂检测天天练系列答案

黄冈金牌之路单元期末卷系列答案

轻负高效系列答案

课时导航系列答案

快乐成长导学案系列答案

快乐练习课时全能练系列答案

相关题目

9．函数f（x）=sinxsin（x+$\frac{π}{3}$）+2cos²x的值域为[$\frac{5-2\sqrt{3}}{4}$，$\frac{5+2\sqrt{3}}{4}$]．

10．某几何体的三视图如图所示，则它的表面积为（　　）

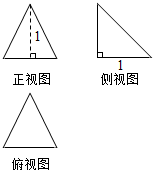
$\frac{{\sqrt{3}+\sqrt{7}+4}}{4}$

$\frac{{\sqrt{6}+2}}{2}$

$\frac{{\sqrt{2}+\sqrt{7}+1}}{2}$

$\frac{{\sqrt{2}+\sqrt{5}+1}}{2}$

7．数列{a_n}的前n项和${S_n}=2{a_n}-3（n∈{N^*}）$，则数列{a_n}的通项公式为a_n=3•2^n-1．

14．根据下列条件．求直线方程：
（1）经过点（3，0）且与直线2x+y-5=0垂直；
（2）经过点B（2，1）且与直线5x+2y+3=0的夹角等于45°．

4．已知定义域为R的函数$f（x）=\frac{{b-{2^x}}}{{{2^{x+1}}+a}}$是奇函数．
（1）求实数a，b的值；
（2）判断f（x）在（-∞，+∞）上的单调性；
（3）若f（k•3^x）+f（3^x-9^x+2）＞0对任意x≥1恒成立，求k的取值范围．

11．下列说法中正确的是（　　）

	A．	“若$\overrightarrow a•\overrightarrow b=0$，则$\overrightarrow a⊥\overrightarrow b$”的否命题是“若$\overrightarrow a•\overrightarrow b≠0$，则$\overrightarrow a⊥\overrightarrow b$”
	B．	命题“?x∈R，恒有x²+1＞0”的否定是“?x₀∈R，使得${x_0}^2+1＜0$”
	C．	?m∈R，使函数f（x）=x²+mx（x∈R）是奇函数
	D．	设p，q是简单命题，若p∧q是真命题，则（￢p）∨q也是真命题

8．已知数列{a_n}习前n顶和为S_n，且满足a₁=1，a_n+2S_nS_n-1=0，（n≥2）
（1）求证：数列{$\frac{1}{{S}_{n}}$}是等差数列．
（2）求{a_n}的通项a_n．

9．在数列{a_n}中，若a₁=$\frac{1}{2}$，a_n=$\frac{1}{1-{a}_{n-1}}$（n≥2，n∈N），则a₂₀₁₂的值为（　　）