题目内容
在△ABC中,若sinA>sinB,则A与B的大小关系为
- A.A>B
- B.A<B
- C.A≥B
- D.A、B的大小关系不能确定
A
分析:解法一:若A,B均为锐角,则A>B;若A,B中有一个为钝角或直角,则只能A为钝角,否则A+B>180°.综上A>B.
解法二:由正弦定理知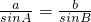 ,由sinA>sinB,知a>b,所以A>B.
,由sinA>sinB,知a>b,所以A>B.
解答:解法一:∵△ABC中,0°<A+B<180°,
∴当0°<A<90°时,
sinA>sinB?A>B.
当90°<A<180°时,
∵sinA>sinB,
A+B<180°,
∴0°<B<90°,
所以A>B.
故选A.
解法二:由正弦定理知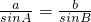 ,
,
∵sinA>sinB,
∴a>b,
∴A>B.
故选A.
点评:本题考查正弦函数的单调性,解题时要认真审题,仔细解答,注意合理地进行等价转化.
分析:解法一:若A,B均为锐角,则A>B;若A,B中有一个为钝角或直角,则只能A为钝角,否则A+B>180°.综上A>B.
解法二:由正弦定理知
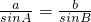 ,由sinA>sinB,知a>b,所以A>B.
,由sinA>sinB,知a>b,所以A>B.解答:解法一:∵△ABC中,0°<A+B<180°,
∴当0°<A<90°时,
sinA>sinB?A>B.
当90°<A<180°时,
∵sinA>sinB,
A+B<180°,
∴0°<B<90°,
所以A>B.
故选A.
解法二:由正弦定理知
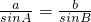 ,
,∵sinA>sinB,
∴a>b,
∴A>B.
故选A.
点评:本题考查正弦函数的单调性,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
在△ABC中,若sinA=
,cosB=
,则cosC的值是( )
| 3 |
| 5 |
| 5 |
| 13 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上都不对 |
在△ABC中,若sinA:sinB:sinC=5:7:8,则此三角形的最大角与最小角之和为( )
| A、90° | B、120° | C、135° | D、150° |