Question

【题目】已知两点分别在轴和轴上运动，且，若动点满足.

（1）求出动点P的轨迹对应曲线C的标准方程；

（2）一条纵截距为2的直线与曲线C交于P，Q两点，若以PQ直径的圆恰过原点，求出直线方程.

Answer 1

【答案】（1）（2）

【解析】试题分析：（1）根据向量的坐标运算，以及|AB|=1，得到椭圆的标准方程．

（2）直线l1斜率必存在，且纵截距为2，根据直线与椭圆的位置关系，即可求出k的值，问题得以解决．

试题解析：

(Ⅰ) 因为

即

所以

所以

又因为,所以

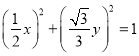即: ,即

所以椭圆的标准方程为

(Ⅱ) 直线斜率必存在，且纵截距为,设直线为

联立直线和椭圆方程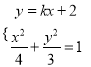

得:

由,得

设

以直径的圆恰过原点

所以,

即

也即

即

将(1)式代入,得

即

解得,满足（*）式，所以

所以直线