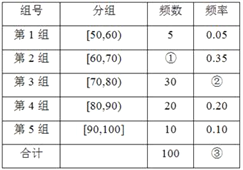
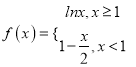题目内容
【题目】设函数
.
（1）求曲线
在点
处的切线方程；
（2）若
在区间
上恒成立，求a的最小值.
【答案】(Ⅰ) 
.(Ⅱ) 
.
【解析】试题分析：（Ⅰ）设切线的斜率为
，利用导数求解切线斜率，然后求解切线方程；（2）要使： 
在区间在
恒成立，等价于： 
在
恒成立，利用函数的导数，通过①当
时，利用
，说明
不满足题意．②当
时，利用导数以及单调性函数的最小值，求解即可.
试题解析：（I）设切线的斜率为
， 
因为
，切点为
.
切线方程为
，化简得： 
.
（II）要使： 
在区间
恒成立，
等价于： 
在
恒成立，
等价于： 
在（0，+∞）恒成立
因为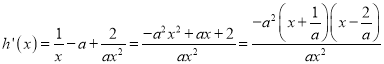
①当
时， 
， 
不满足题意
②当
时，令
，则
或
（舍）.
所以
时
， 
在
上单调递减；
时
， 
在
上单调递增；
当
时
当
时，满足题意
所以
，得到
的最小值为
练习册系列答案
相关题目
