题目内容
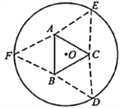
【题目】如图，圆形纸片的圆心为O，半径为5 cm，该纸片上的等边三角形ABC的中心为O.D、E、F为圆O上的点，△DBC，△ECA，△FAB分别是以BC，CA，AB为底边的等腰三角形.沿虚线剪开后，分别以BC，CA，AB为折痕折起△DBC，△ECA，△FAB，使得D、E、F重合，得到三棱锥.当△ABC的边长变化时，所得三棱锥体积（单位：cm3）的最大值为( )
A. 
B. 
C. 
D. 
【答案】D
【解析】
由题意，连接OD，交BC于点G，由题意得OD⊥BC，OG=
BC，
即OG的长度与BC的长度成正比，
设OG=x，则BC=2
x，DG=5﹣x，
三棱锥的高h=
， 
，
则V=
，
令f（x）=25x4﹣10x5，x∈（0， 
），f′（x）=100x3﹣50x4，
令f′（x）=0，即x4﹣2x3=0，解得x=2，
f（x）在
上单调递增，在
上单调递减
∴f（x）≤f（2）=80，
∴V≤
，∴体积最大值为
．
故选： 
．
练习册系列答案
相关题目
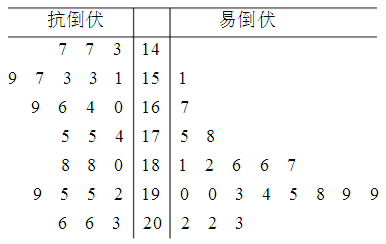
【题目】某港口有一个泊位，现统计了某月100艘轮船在该泊位停靠的时间（单位：小时），如果停靠时间不足半小时按半小时计时，超过半小时不足1小时按1小时计时，以此类推，统计结果如表：
停靠时间 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 |
轮船数量 | 12 | 12 | 17 | 20 | 15 | 13 | 8 | 3 |
（Ⅰ）设该月100艘轮船在该泊位的平均停靠时间为
小时，求
的值；
（Ⅱ）假定某天只有甲、乙两艘轮船需要在该泊位停靠
小时，且在一昼夜的时间段中随机到达，求这两艘轮船中至少有一艘在停靠该泊位时必须等待的概率．
