题目内容
点 在同一个球的球面,
在同一个球的球面, ,
,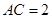 ,若四面体
,若四面体 体积的最大值为
体积的最大值为 ,则这个球的表面积为( )
,则这个球的表面积为( )
A. | B. | C. | D. |
C
解析试题分析:∵ ,∴
,∴ 是直角三角形,
是直角三角形,
∴  的外接圆的圆心是边AC的中点O1,如图所示,若使四面体ABCD体积的最大值只需使点D到平面ABC的距离最大,又
的外接圆的圆心是边AC的中点O1,如图所示,若使四面体ABCD体积的最大值只需使点D到平面ABC的距离最大,又 平面ABC,所以点D是直线
平面ABC,所以点D是直线 与球的交点设球的半径为R,则由体积公式有:
与球的交点设球的半径为R,则由体积公式有: 在
在 中,
中, ,
,
解得:
 ,故选C。
,故选C。
考点:本题主要考查球的性质,四面体的几何特征,几何体体积计算,球的表面积。
点评:中档题,实际上是球内接四面体问题,利用球的性质,四面体的几何特征,体积计算等,确定球的半径,进一步得到球的表面积

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知圆锥的正视图是边长为2的等边三角形,则该圆锥体积为 ( )
A. | B. | C. | D. |
一个几何体的三视图如右图所示,则该几何体的体积为( )
| A.16 | B.12 | C.8 | D.4 |
某几何体的三视图如下,则几何体的表面积为( )
A.28+6 | B.30+6 | C.56+12 | D.60+12 |
某几何体的三视图如下图所示,则该几何体为( )
| A.三棱柱 | B.三棱锥 | C.圆锥 | D.四棱锥 |
某几何体的三视图如图,则该几何体的表面积为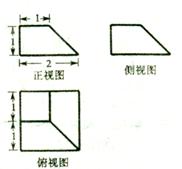
A. | B. |
C. | D. |





 . 则
. 则 的外接圆的面积为
的外接圆的面积为






