题目内容
某几何体的三视图如图,则该几何体的表面积为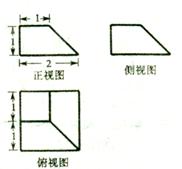
A. | B. |
C. | D. |
B
解析试题分析:根据题意可知该三视图还原为几何体为长方体截取了两个四棱锥剩下的部分,因为底面的边长为2的正方形,高为1,侧面是梯形,上底面积为1,下底面积为4,那么侧面积为上底为1,下底为2,高为 的两个等腰梯形,加上矩形2的面积即为所求,故结果为
的两个等腰梯形,加上矩形2的面积即为所求,故结果为 ,选B.
,选B.
考点:三视图的运用
点评:解决的关键是根据三视图还原几何体,通过几何体的表面积公式来得到求解,属于基础题。

练习册系列答案
相关题目
点 在同一个球的球面,
在同一个球的球面, ,
,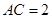 ,若四面体
,若四面体 体积的最大值为
体积的最大值为 ,则这个球的表面积为( )
,则这个球的表面积为( )
A. | B. | C. | D. |
棱长为1的正方体ABCD-A1B1C1D1中,四面体AB1CD1的体积为( )
A. | B. | C.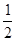 | D. |
平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为 ,则此球的体积为
,则此球的体积为
A. π π | B.4 π π | C.4 π π | D.6 π π |
一个空间几何体的三视图如右图所示,其中主视图和侧视图都是半径为 的圆,且这个几何体是球体的一部分,则这个几何体的表面积为( ).
的圆,且这个几何体是球体的一部分,则这个几何体的表面积为( ).
| A.3π | B.4π | C.6π | D.8π |
 的正三角形,其俯视图是边长为2
的正三角形,其俯视图是边长为2





 ,
, ,则函数
,则函数

 为正三角形,
为正三角形, ,
, ,且
,且

 ,则多面体
,则多面体 的正视图(也称主视图)是( )
的正视图(也称主视图)是( )
 的各顶点都在一个半径为
的各顶点都在一个半径为 的球面上,球心
的球面上,球心 在
在 上,
上, 底面
底面 ,
,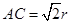 ,则球的体积与三棱锥体积之比是( )
,则球的体积与三棱锥体积之比是( )