题目内容
已知函数f(x)=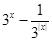 .
.
(1)若f(x)=2,求x的值;
(2)判断x>0时,f(x)的单调性;
(3)若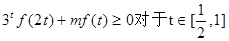 恒成立,求m的取值范围。
恒成立,求m的取值范围。
(1) x=log3(1+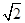 ) ;
) ;
(2) f(x)=3x-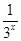 在(0,+∞)上单调递增 ;
在(0,+∞)上单调递增 ;
(3) [-4,+∞).
解析试题分析:(1)当x≤0时,f(x)=3x-3x=0,∴f(x)=2无解.
当x>0时,f(x)=3x-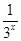 ,令3x-
,令3x-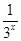 =2,
=2,
∴(3x)2-2·3x-1=0,∴3x=1±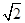 .
.
∵3x>0,∴3x=1-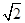 (舍).∴3x=1+
(舍).∴3x=1+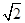 .∴x=log3(1+
.∴x=log3(1+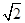 ) 4分
) 4分
(2)当x>0,f(x)=3x-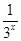 .∵y=3x在(0,+∞)上单调递增,
.∵y=3x在(0,+∞)上单调递增,
y=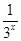 在(0,+∞)上单调递减.
在(0,+∞)上单调递减.
∴f(x)=3x-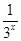 在(0,+∞)上单调递增 8分
在(0,+∞)上单调递增 8分
(3)∵t∈[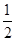 ,1],∴f(t)=3t-
,1],∴f(t)=3t-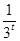 >0,
>0,
∴3tf(2t)+mf(t)≥0化为3t(32t-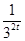 )+m(3t-
)+m(3t-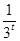 )≥0.
)≥0.
即3t(3t+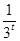 )+m≥0.即m≥-32t-1.
)+m≥0.即m≥-32t-1.
令g(t)=-32t-1,则g(t)在[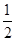 ,1]上递减,
,1]上递减,
∴g(x)max=-4.
∴所求实数m的取值范围是[-4,+∞) 13分
考点:本题主要考查指数函数的性质,指数方程的解法,不等式恒成立问题。
点评:中档题,解简单的指数方程,一般是考虑化同底数指数幂相等或利用“换元法”,转化成一元二次方程求解。不等式恒成立问题,一般是利用“分离参数法”,转化成求函数最值问题。

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
 .
.  处取到极值?若有可能,求实数
处取到极值?若有可能,求实数 的值;否则说明理由;
的值;否则说明理由; 上为增函数,求实数
上为增函数,求实数 ,其中
,其中 ,
, .
. 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程; 的单调区间.(要写推理过程)
的单调区间.(要写推理过程) ,g(x)=2|x|+a.
,g(x)=2|x|+a. ,
,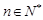 ,其导函数记为
,其导函数记为 ,
, ,求
,求 的极大值与极小值;
的极大值与极小值; 的方程
的方程 在区间
在区间 上的实数根的个数。
上的实数根的个数。
 时,求
时,求 的解集
的解集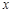 的不等式
的不等式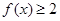 的解集是
的解集是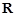 ,求
,求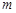 的取值范围
的取值范围 满足:g(2)=4,定义域为
满足:g(2)=4,定义域为 的函数
的函数 是奇函数。
是奇函数。 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围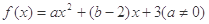 ,若不等式
,若不等式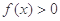 的解集为
的解集为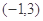 .(Ⅰ)求
.(Ⅰ)求 的值;(Ⅱ)若函数
的值;(Ⅱ)若函数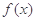 在
在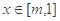 上的最小值为1,求实数
上的最小值为1,求实数 的值.
的值. ,其中
,其中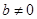 .
.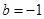 时,求在曲线
时,求在曲线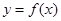 上一点
上一点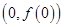 处的切线方程;
处的切线方程;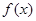 的极值点。
的极值点。