题目内容
已知指数函数 满足:g(2)=4,定义域为
满足:g(2)=4,定义域为 的函数
的函数 是奇函数。
是奇函数。
(1)确定 的解析式;(2)求m,n的值;
的解析式;(2)求m,n的值;
(3)若对任意的 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围
(1)m=2,n=1(2)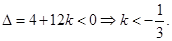
解析试题分析:解:(1) 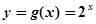 2分
2分
(2)由(1)知: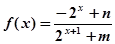
因为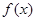 是奇函数,所以
是奇函数,所以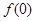 =0,即
=0,即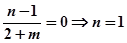
∴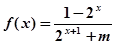 , 又由f(1)= -f(-1)知
, 又由f(1)= -f(-1)知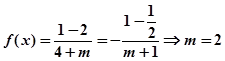 3分
3分
(3)由(2)知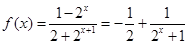 ,
,
易知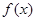 在
在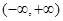 上为减函数。
上为减函数。
又因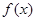 是奇函数,从而不等式:
是奇函数,从而不等式:  等价于
等价于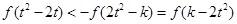 ,
,
因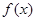 为减函数,由上式推得:
为减函数,由上式推得: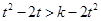
即对一切 有:
有: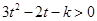 ,
,
从而判别式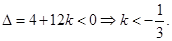 5分
5分
考点:函数奇偶性和单调性的运用
点评:主要是考查了函数的奇偶性和单调性的性质的综合运用,结合概念来判定,并解不等式,属于中档题。

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目

 时,求
时,求 在[1,
在[1, ]上的取值范围。
]上的取值范围。 在[1,
在[1,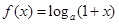 ,
,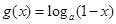 ,其中
,其中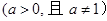 ,设
,设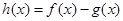 .
. 的定义域;
的定义域; ,求使
,求使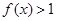 成立的
成立的 的集合.
的集合.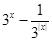 .
.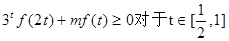 恒成立,求m的取值范围。
恒成立,求m的取值范围。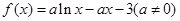 .
.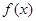 的单调区间
的单调区间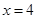 处切线的斜率为
处切线的斜率为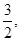 若函数
若函数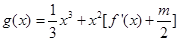 在区间(1,3)上不是单调函数,求m的取值范围
在区间(1,3)上不是单调函数,求m的取值范围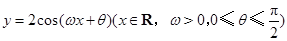 的图象与
的图象与 轴相交于点
轴相交于点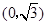 ,且该函数的最小正周期为
,且该函数的最小正周期为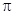 .
.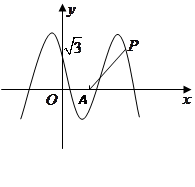
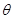 和
和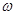 的值;
的值;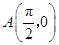 ,点
,点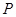 是该函数图象上一点,
是该函数图象上一点,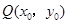 是
是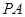 的中点,当
的中点,当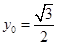 ,
,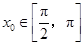 时,求
时,求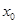 的值.
的值.  是定义在
是定义在 上的函数,当
上的函数,当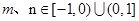 ,且
,且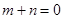 时,有
时,有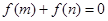 .
.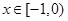 时,
时, (a为实数). 则当
(a为实数). 则当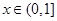 时,求
时,求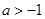 时,试判断
时,试判断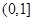 上的单调性,并证明你的结论.
上的单调性,并证明你的结论.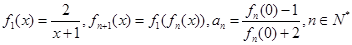
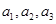 ,并求数列
,并求数列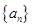 的通项公式.
的通项公式. 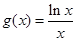 在
在 上为减函数,设数列
上为减函数,设数列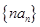 的前
的前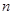 的和为
的和为 ,
,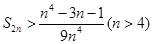
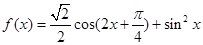 .
.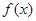 的最小正周期;
的最小正周期;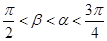 ,且
,且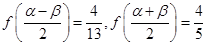 ,求
,求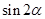 的值.
的值.