题目内容
对于两个正数a1,a2而言,则有| 2 | ||||||||
|
| a1 a2 |
| a1+a2 |
| 2 |
|
| 3 | ||||||
|
| 3 | a1a2a3 |
| a1+a2+a3 |
| 3 |
|
分析:本题考查的知识点是归纳推理,我们可以根据已知条件中的不等式,分析不等式两边的各项和式及指数部分与式子编号之间的关系,易得不等式的分子分母的系数,归纳后即可推断出第n(n∈N*)个不等式.
解答:解:由已知中的式了,我们观察后分析:
不等式组有四个式子组成,
左边的第一个为
,
左边的第二个为
不等式右边第一个为
不等式右边第二个为
根据已知可以推断:
第n(n∈N*)个不等式为:
≤
≤
≤
故答案为:
≤
≤
≤
不等式组有四个式子组成,
左边的第一个为
| n | ||||||||
|
左边的第二个为
| n | a1a2a3… an |
不等式右边第一个为
|
不等式右边第二个为
| a1+a2+a3+…+an |
| n |
根据已知可以推断:
第n(n∈N*)个不等式为:
| n | ||||||||
|
| n | a1a2a3… an |
| a1+a2+a3+…+an |
| n |
|
故答案为:
| n | ||||||||
|
| n | a1a2a3… an |
| a1+a2+a3+…+an |
| n |
|
点评:本题考查归纳推理,由不等式构造新不等式的能力.本题题目的注意事项是:一、四个式子的结构特征,二、四个式子的大小关系;三、分子分母及要根指数的相应变化.

练习册系列答案
相关题目
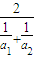 ≥
≥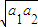 ≤
≤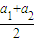 ≤
≤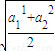 成立;对于三个正数a1,a2,a3而言,则有
成立;对于三个正数a1,a2,a3而言,则有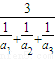 ≤
≤ ≤
≤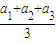 ≤
≤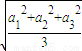 成立;那么对于n个正数a1,a2,a3…an而言,则 成立.
成立;那么对于n个正数a1,a2,a3…an而言,则 成立. =
= ≤
≤ ≤
≤ 成立;对于三个正数a1,a2,a3而言,则有
成立;对于三个正数a1,a2,a3而言,则有 ≤
≤ ≤
≤ ≤
≤ 那么对于n个正数a1,a2,a3…an而言,则有 成立.
那么对于n个正数a1,a2,a3…an而言,则有 成立.