题目内容
对于两个正数a1,a2而言,则有| 2 | ||||
|
| a1a2 |
| a1+a2 |
| 2 |
|
| 3 | ||||||
|
| 3 | a1 a2a3 |
| a1+a2+a3 |
| 3 |
|
分析:观察所给的两个不等式链,前三个是基本不等式中出现过的不等式,第四个是所给的整数的平方和的算术平均数的算术平方根,写出含有n个正数的不等式链.
解答:解:根据所给的两个正数和三个正数的关系式,
得到这是一组不等式链,
前三个是基本不等式中出现过的,第四个是所给的整数的平方和的算术平均数的算术平方根,
∴写出由n个整数形成的不等式链是:
≤
≤
≤
故答案为:
≤
≤
≤
得到这是一组不等式链,
前三个是基本不等式中出现过的,第四个是所给的整数的平方和的算术平均数的算术平方根,
∴写出由n个整数形成的不等式链是:
| n | ||||||
|
| n | a1a2…an |
| a1+a2+…+an |
| n |
|
故答案为:
| n | ||||||
|
| n | a1a2…an |
| a1+a2+…+an |
| n |
|
点评:本题考查类比推理,考查根据所给的不等式链写出符合条件的不等式,本题考查学生对于所学的基本不等式的理解,和对于新内容的理解,本题是一个易错题.

练习册系列答案
相关题目
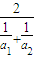 ≥
≥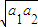 ≤
≤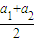 ≤
≤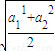 成立;对于三个正数a1,a2,a3而言,则有
成立;对于三个正数a1,a2,a3而言,则有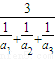 ≤
≤ ≤
≤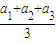 ≤
≤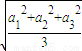 成立;那么对于n个正数a1,a2,a3…an而言,则 成立.
成立;那么对于n个正数a1,a2,a3…an而言,则 成立. =
= ≤
≤ ≤
≤ 成立;对于三个正数a1,a2,a3而言,则有
成立;对于三个正数a1,a2,a3而言,则有 ≤
≤ ≤
≤ ≤
≤ 那么对于n个正数a1,a2,a3…an而言,则有 成立.
那么对于n个正数a1,a2,a3…an而言,则有 成立.