题目内容
已知α∈( ,π),sinα=
,π),sinα= ,则
,则 等于
等于
- A.

- B.

- C.

- D.
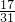
B
分析:由α的范围及sinα的值,根据同角三角函数间的基本关系求出cosα的值,进而求出tanα的值,然后利用二倍角的正切函数公式表示出tan2α,把tanα的值代入求出tan2α的值,最后把所求的式子利用两角和的正切函数公式及特殊角的三角函数值化简,将tan2α的值代入即可求出值.
解答:由α∈( ,π),sinα=
,π),sinα= ,得到cosα=-
,得到cosα=- ,
,
∴tanα=- ,∴tan2α=
,∴tan2α=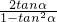 =
= =-
=-
则tan(α+ )=
)= =
= =-
=-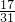 .
.
故选B
点评:此题考查了二倍角的正切函数公式,两角和与差的正切函数公式及同角三角函数间的基本关系.熟练掌握公式是解本题的关键.
分析:由α的范围及sinα的值,根据同角三角函数间的基本关系求出cosα的值,进而求出tanα的值,然后利用二倍角的正切函数公式表示出tan2α,把tanα的值代入求出tan2α的值,最后把所求的式子利用两角和的正切函数公式及特殊角的三角函数值化简,将tan2α的值代入即可求出值.
解答:由α∈(
 ,π),sinα=
,π),sinα= ,得到cosα=-
,得到cosα=- ,
,∴tanα=-
 ,∴tan2α=
,∴tan2α=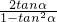 =
= =-
=-
则tan(α+
 )=
)= =
= =-
=-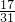 .
.故选B
点评:此题考查了二倍角的正切函数公式,两角和与差的正切函数公式及同角三角函数间的基本关系.熟练掌握公式是解本题的关键.

练习册系列答案
相关题目