题目内容
(本题满分16分)已知函数 .
.
(1)若 ,解方程
,解方程 ;
;
(2)若函数 在
在 上单调递增,求实数
上单调递增,求实数 的取值范围;
的取值范围;
(3)若 且不等式
且不等式 对一切实数
对一切实数 恒成立,求
恒成立,求 的取值范围
的取值范围
(1) 或
或 ;(2)
;(2) ;(3)
;(3)
【解析】
试题分析:(1)当 时
时 ;再分类讨论解方程可得解集为
;再分类讨论解方程可得解集为 或
或 ;(2)
;(2) ,若
,若 在
在 上单调递增,利用分段函数及二次函数的性质则有
上单调递增,利用分段函数及二次函数的性质则有
 ;(3)设
;(3)设 即不等式
即不等式 对一切实数
对一切实数 恒成立,因
恒成立,因 ,通过计算知当
,通过计算知当 时,
时, ;当
;当 时,因
时,因 ,故
,故 ,
, ,可得
,可得 ,综上
,综上
试题解析:(1)当 时,有
时,有 2分
2分
当 时,
时, ,解得:
,解得: 或
或
当 时,
时, 恒成立 4分
恒成立 4分
∴方程的解集为: 或
或 5分
5分
(2) 7分
7分
若 在
在 上单调递增,则有
上单调递增,则有 ,解得:
,解得: 10分
10分
(3)设 ,则
,则
即不等式 对一切实数
对一切实数 恒成立 11分
恒成立 11分
∵
∴当 时,
时, 单调递减,其值域为:
单调递减,其值域为: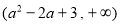
∵ ,∴
,∴ 恒成立 13分
恒成立 13分
当 时,∵
时,∵ ,∴
,∴ ,
,
∴ ,得
,得
∵ ,∴
,∴ 15分
15分
综上: 16分
16分
考点:函数及其性质的综合应用

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 上单调递增的是( )
上单调递增的是( )



 的定义域为
的定义域为 (B)
(B) (C)
(C) (D)
(D)
 ,满足
,满足 ,且对任意的
,且对任意的 都有
都有 ,则
,则 (7)=____________;
(7)=____________; .
. 是定义在R上的周期为3的函数,当
是定义在R上的周期为3的函数,当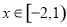 时,
时,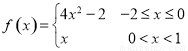 ,则
,则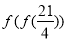 =( )
=( )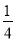 B.
B.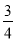 C.
C. D.0
D.0
 ,则
,则 的取值范围是 .
的取值范围是 . 是定义在
是定义在 上的增函数,函数
上的增函数,函数 的图象关于点(1,0)对称,若对任意的
的图象关于点(1,0)对称,若对任意的 ,
,
 ,等式
,等式 恒成立,则
恒成立,则 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.
 }的前
}的前 项和为
项和为 ,若
,若 ,则满足
,则满足 的正整数
的正整数 .
. 的图象为( )
的图象为( ) B.
B. C.
C. D.
D.