题目内容
已知函数f（x）=|x-2|+|x+2|．
（1）利用分段函数的形式表示f（x）；【提示：零点分段法】
（2）画出函数f（x）的图象；
（3）根据图象写出f（x）的单调区间．
（1）利用分段函数的形式表示f（x）；【提示：零点分段法】
（2）画出函数f（x）的图象；
（3）根据图象写出f（x）的单调区间．
考点：分段函数的应用
专题：数形结合,函数的性质及应用
分析：（1）利用零点分段示，我们分析求出函数的解析式，进而可以用分段函数的形式表示该函数；
（2）根据分段函数分段画的原则，我们根据（1）的解析式，分别画出对应函数的图象，综合后即可得到该函数的图象；
（3）根据（2）中函数的图象，我们可以得到函数的单调区间．
（2）根据分段函数分段画的原则，我们根据（1）的解析式，分别画出对应函数的图象，综合后即可得到该函数的图象；
（3）根据（2）中函数的图象，我们可以得到函数的单调区间．
解答：解：（1）∵f（x）=|x-2|+|x+2|．
∴f（x）=
（2）由（1）可得函数的图象如下图所示：
（3）由图可得，函数的单调增区间（2，+∞），单调减区间（-∞，-1）．
∴f（x）=
|
（2）由（1）可得函数的图象如下图所示：
（3）由图可得，函数的单调增区间（2，+∞），单调减区间（-∞，-1）．
点评：本题考查的知识点是分段函数的解析式求法及其图象的作法，函数的定义域及其求法，函数的值域，函数的图象，其中利用零点分段法求出函数的解析式是解答本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
函数y=loga（x-1）+2（a＞0，a≠1）的图象恒过点（ ）
| A、（1，2） | B、（2，2） | C、（2，3） | D、（4，4） |
已知函数f（x）=
，若f（a）=1，则a的所有可能结果之和为（ ）
|
| A、e | ||
B、
| ||
C、e+
| ||
D、2e+
|
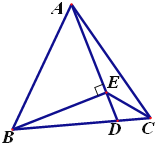如图，△ABC是边长为2的等边三角形，D是边BC上的动点，BE⊥AD于E，则CE的最小值为（ ）| A、1 | ||||
B、2-
| ||||
C、
| ||||
D、
|
正四棱锥S-ABCD中，SA=AB，则直线AC与平面SBC所成角的正弦值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
某程序框图如图所示，现输入如下四个函数，则可以输出的函数是（ ）
| A、f（x）=x•tanx | ||
| B、f（x）=x2+1 | ||
C、f（x）=x2+
| ||
| D、f（x）=x3•cosx |