题目内容
2．△ABC的内角A，B，C的对边分别为a，b，c，已知a=2$\sqrt{5}$，c=4，cosA=$\frac{2}{3}$，则b=（ ）| A． | 2$\sqrt{2}$ | B． | 2$\sqrt{5}$ | C． | 4 | D． | 6 |
分析 由已知利用余弦定理即可计算得解．
解答 解：∵a=2$\sqrt{5}$，c=4，cosA=$\frac{2}{3}$，
∴由余弦定理a2=b2+c2-2bccosA，可得：20=b2+16-2×$b×4×\frac{2}{3}$，
∴整理可得：3b2-16b-12=0，解得：b=6或-$\frac{2}{3}$（舍去）．
故选：D．
点评 本题主要考查了余弦定理在解三角形中的应用，属于基础题．
练习册系列答案
相关题目
2．过点（2，2）的直线l与圆x2+y2+2x-2y-2=0相交于A，B两点，且$|{AB}|=2\sqrt{3}$，则直线l的方程为（ ）
| A． | 3x-4y+2=0 | B． | 3x-4y+2=0，或x=2 | C． | 3x-4y+2=0，或y=2 | D． | y=2，或x=2 |
10．
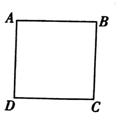如图，正方形ABCD边长为1，从某时刻起，将线段AB，BC，CD，DA分别绕点A，B，C，D顺时针旋转相同角度α（0＜α＜$\frac{π}{2}$），若旋转后的四条线段所围成的封闭图形面积为$\frac{1}{2}$，则α=（ ）
如图，正方形ABCD边长为1，从某时刻起，将线段AB，BC，CD，DA分别绕点A，B，C，D顺时针旋转相同角度α（0＜α＜$\frac{π}{2}$），若旋转后的四条线段所围成的封闭图形面积为$\frac{1}{2}$，则α=（ ）| A． | $\frac{π}{12}$或$\frac{5π}{12}$ | B． | $\frac{π}{12}$或$\frac{π}{3}$ | C． | $\frac{π}{6}$或$\frac{5π}{12}$ | D． | $\frac{π}{6}$或$\frac{π}{3}$ |
17．△ABC中，若a=1，b=2，sinA=$\frac{1}{3}$，则sinB=（ ）
| A． | $\frac{2}{3}$ | B． | $\frac{1}{3}$ | C． | $\frac{\sqrt{2}}{3}$ | D． | $\frac{\sqrt{2}}{6}$ |
14．直线y=2x-3在y轴上的截距是（ ）
| A． | 3 | B． | 2 | C． | -2 | D． | -3 |