题目内容
(本小题满分12分)
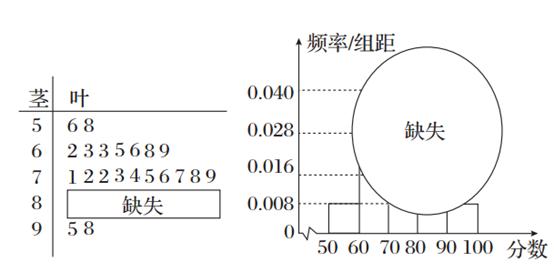
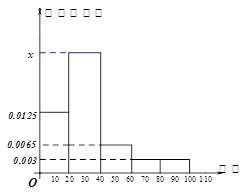
从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下图频率分布直方图:
(I)求这500件产品质量指标值的样本平均值 和样本方差
和样本方差 (同一组的数据用该组区间的中点值作代表);
(同一组的数据用该组区间的中点值作代表);
(II)由直方图可以认为,这种产品的质量指标 服从正态分布
服从正态分布 ,其中
,其中 近似为样本平均数
近似为样本平均数 ,
, 近似为样本方差
近似为样本方差 .
.
(i)利用该正态分布,求 ;
;
(ii)某用户从该企业购买了100件这种产品,记 表示这100件产品中质量指标值位于区间
表示这100件产品中质量指标值位于区间 的产品件数.利用(i)的结果,求
的产品件数.利用(i)的结果,求 .
.
附:
若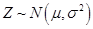 则
则 ,
, 。
。
(I) ;(II)(i)
;(II)(i) ;(ii)
;(ii) .
.
解析试题分析:(I)由频率分布直方图可估计样本特征数众数、中位数、均值、方差.若同一组的数据用该组区间的中点值作代表,则众数为最高矩形中点横坐标.中位数为面积等分为 的点.均值为每个矩形中点横坐标与该矩形面积积的累加值.方差是矩形横坐标与均值差的平方的加权平均值.(II)(i)由已知得,
的点.均值为每个矩形中点横坐标与该矩形面积积的累加值.方差是矩形横坐标与均值差的平方的加权平均值.(II)(i)由已知得,
 ,故
,故

 ;(ii)某用户从该企业购买了100件这种产品,相当于100次独立重复试验,则这100件产品中质量指标值位于区间
;(ii)某用户从该企业购买了100件这种产品,相当于100次独立重复试验,则这100件产品中质量指标值位于区间 的产品件数
的产品件数 ,故期望
,故期望 .
.
试题分析:(I)抽取产品的质量指标值的样本平均值 和样本方差
和样本方差 分别为
分别为


 ,
,
 .
.
(II)(i)由(I)知, 服从正态分布
服从正态分布 ,从而
,从而

 .
.
(ii)由(i)可知,一件产品的质量指标值位于区间 的概率为
的概率为 ,依题意知
,依题意知 ,所以
,所以 .
.
【考点定位】1、频率分布直方图;2、正态分布的 原则;3、二项分布的期望.
原则;3、二项分布的期望.

练习册系列答案
相关题目
某地区2007年至2013年农村居民家庭纯收入y(单位:千元)的数据如下表:
| 年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
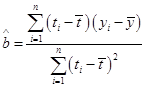 ,
,
为了了解调研高一年级新学生的智力水平,某校按l 0%的比例对700名高一学生按性别分别进行“智力评分”抽样检查,测得“智力评分”的频数分布表如下表l,表2.
表1:男生“智力评分”频数分布表
| 智力评分 | 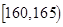 | 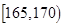 | 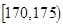 | 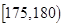 | 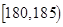 | 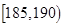 |
| 频数 | 2 | 5 | 14 | 13 | 4 | 2 |
表2:女生“智力评分”频数分布表
| 智力评分 | 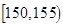 | 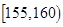 | 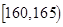 | 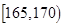 | 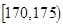 | 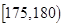 |
| 频数 | 1 | 7 | 12 | 6 | 3 | 1 |
(1)求高一的男生人数并完成下面男生的频率分布直方图;
(2)估计该校学生“智力评分”在[1 65,1 80)之间的概率;
(3)从样本中“智力评分”在[180,190)的男生中任选2人,求至少有1人“智力评分”在[185,190)之间的概率.
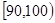 ,第二组
,第二组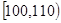 , ,第五组
, ,第五组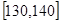 .按上述分组
.按上述分组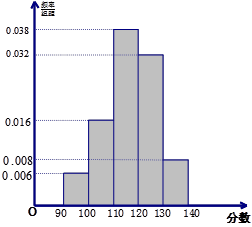
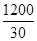 =40;
=40; ,样本数据分组为
,样本数据分组为 ,
,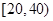 ,
,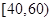 ,
,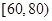 ,
,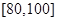 .
.
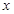 的值;
的值; 元/张
元/张 ,则“足球迷”中非“铁杆足球迷”愿意前往观看的人数会减少
,则“足球迷”中非“铁杆足球迷”愿意前往观看的人数会减少 ,“铁杆足球迷”愿意前往观看的人数会减少
,“铁杆足球迷”愿意前往观看的人数会减少 .问票价至少定为多少元/张时,才能使前往现场观看足球比赛的人数不超过10万人?
.问票价至少定为多少元/张时,才能使前往现场观看足球比赛的人数不超过10万人?
 名网友4月1日这天的网购情况,得到如下数据统计表(图(1))网购金额超过
名网友4月1日这天的网购情况,得到如下数据统计表(图(1))网购金额超过 千元的顾客被定义为“网购红人”,网购金额不超过
千元的顾客被定义为“网购红人”,网购金额不超过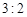 .
.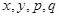 的值,并补全频率分布直方图(图(2)).
的值,并补全频率分布直方图(图(2)).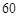 名网友的购物体验,从“非网购红人”和“网购红人”中用分层抽样的方法确定
名网友的购物体验,从“非网购红人”和“网购红人”中用分层抽样的方法确定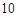 人,若需从这
人,若需从这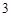 人进行问卷调查,设
人进行问卷调查,设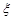 为选取的
为选取的