题目内容
两个球的体积之比为8:27,则它们的表面积的比是( )
| A、2:3 | ||||
B、
| ||||
| C、4:9 |
考点:球的体积和表面积
专题:空间位置关系与距离
分析:设两个球的半径分别为R,r,由体积比得到半径比,那么表面积比等于半径的平方比.那么两个球的体积比为
πR3:
πr3=8:27
| 4 |
| 3 |
| 4 |
| 3 |
解答:
解:设两个球的半径分别为R,r,那么两个球的体积比为
πR3:
πr3=8:27,所以R:r=2:3,
所以它们的表面积的比是4πR2:4πr2=R2:r2=4:8;
故选C.
| 4 |
| 3 |
| 4 |
| 3 |
所以它们的表面积的比是4πR2:4πr2=R2:r2=4:8;
故选C.
点评:本题考查了球的表面积和体积公式;两个球的表面积比等于半径的平方比,体积比等于半径的立方比.

练习册系列答案
相关题目
设曲线y=
在点(3,2)处的切线与直线ax-y+1=0平行,则a=( )
| x+1 |
| x-1 |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
经过空间任意三点作平面( )
| A、只有一个 |
| B、可作二个 |
| C、可作无数多个 |
| D、只有一个或有无数多个 |
 已知抛物线x2=4y,过原点作斜率为1的直线交抛物线于第一象限内一点P1,又过点P1作斜率为
已知抛物线x2=4y,过原点作斜率为1的直线交抛物线于第一象限内一点P1,又过点P1作斜率为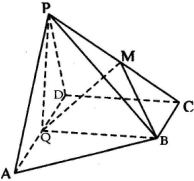 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,BC=