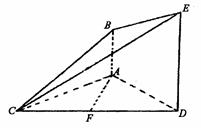
题目内容
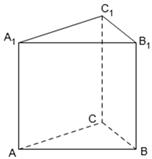
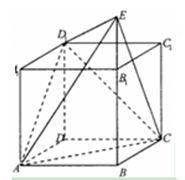
如图,在三棱柱 中,
中,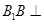 平面
平面 ,
, ,
,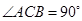 ,
, 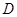 ,
, 分别是
分别是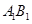 ,
, 的中点.
的中点.
(Ⅰ)求证: ∥平面
∥平面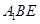 ;
;
(Ⅱ)求证:平面 平面
平面 ;
;
(Ⅲ)求直线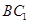 与平面
与平面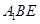 所成角的正弦值.
所成角的正弦值.
(Ⅰ)详见解析;(Ⅱ)详见解析;(Ⅲ)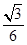
解析试题分析:(Ⅰ)根据题意可根据中点证平行四边形得线线平行,再根据线面平行的性质定理得线面平行。(Ⅱ)由已知条件易得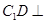 平面
平面 .由(Ⅰ)知
.由(Ⅰ)知 ∥
∥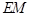 ,即
,即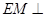 平面
平面 。根据面面垂直的判定定理可得平面
。根据面面垂直的判定定理可得平面 平面
平面 。(Ⅲ)法一普通方法:可用等体积法求点
。(Ⅲ)法一普通方法:可用等体积法求点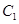 到面
到面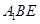 的距离,再用线面角的定义找到线面角后求其正弦值。此法涉及到大量的计算,过程较繁琐;法二空间向量法:建立空间直角坐标系后先求面
的距离,再用线面角的定义找到线面角后求其正弦值。此法涉及到大量的计算,过程较繁琐;法二空间向量法:建立空间直角坐标系后先求面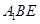 的法向量。
的法向量。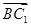 与法向量所成角余弦值的绝对值即为直线
与法向量所成角余弦值的绝对值即为直线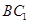 与平面
与平面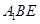 所成角的正弦值。
所成角的正弦值。
试题解析:证明:(Ⅰ)
取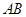 的中点
的中点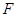 ,连结
,连结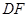 ,交
,交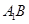 于点
于点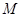 ,可知
,可知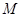 为
为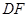 中点,
中点,
连结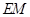 ,易知四边形
,易知四边形 为平行四边形,
为平行四边形,
所以 ∥
∥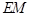 .
.
又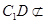 平面
平面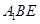 ,
,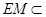 平面
平面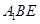 ,
,
所以 ∥平面
∥平面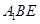 . 4分
. 4分
证明:(Ⅱ)因为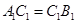 ,且
,且 是
是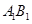 的中点,
的中点,
所以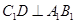 .
.
因为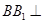 平面
平面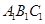 ,所以
,所以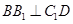 .
.
所以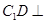 平面
平面 .
.
又 ∥
∥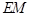 ,所以
,所以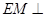 平面
平面 .
.
又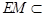 平面
平面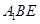 ,
,
所以平面 平面
平面 . 9分
. 9分
解:(Ⅲ)如图建立空间直角坐标系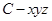 ,
,
则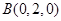 ,
,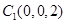 ,
, 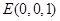 ,
,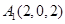 .
.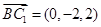 ,
,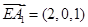 ,
,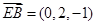 .
.
设平面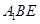 的法向量为
的法向量为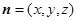 .
.
则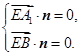
所以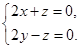
令 .则
.则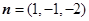 .
.
设向量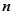 与
与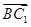 的夹角为
的夹角为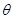 ,则
,则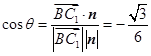 .
.
所以直线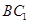 与平面
与平面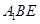 所成角的正弦值为
所成角的正弦值为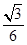 . 14分
. 14分
考点:1线线平行、线面平行;2线线垂直、线面垂直;3线面角。

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
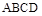 与
与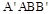 都是边长为
都是边长为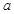 的正方形,点E是
的正方形,点E是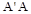 的中点,
的中点,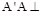 平面
平面
 平面
平面 ;
; 平面
平面 中,
中, 是正方形,
是正方形,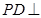 平面
平面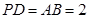 ,
,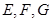 分别是
分别是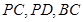 的中点.
的中点.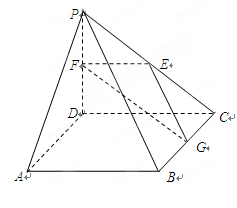
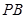 上确定一点
上确定一点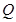 ,使
,使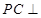 平面
平面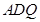 ,并给出证明;
,并给出证明; 平面
平面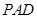 ,并求出
,并求出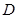 到平面
到平面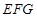 的距离.
的距离.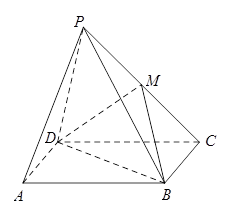
 中,点
中,点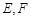 分别是棱
分别是棱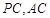 的中点.
的中点.
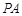 //平面
//平面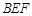 ;
;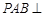 平面
平面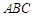 ,
,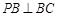 ,求证:
,求证: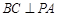 .
.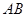 是圆的直径,
是圆的直径,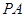 垂直圆所在的平面,
垂直圆所在的平面, 是圆上任一点,
是圆上任一点,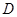 是线段
是线段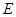 是线段
是线段 上的一点.
上的一点.
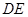 ∥平面
∥平面 ;
;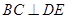 .
. 、
、 、
、 为不在同一直线上的三点,且
为不在同一直线上的三点,且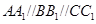 ,
,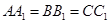 .
.
 //平面
//平面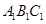 ;
;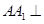 平面
平面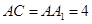 ,
,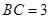 ,
,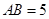 ,求证:
,求证: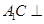 平面
平面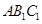 ;
;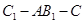 的余弦值.
的余弦值.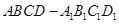 中,底面
中,底面 为菱形,且
为菱形,且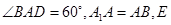 为
为 延长线上的一点,
延长线上的一点,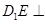 面
面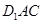 .设
.设 .
.
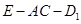 的大小;
的大小; 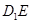 上是否存在一点
上是否存在一点 ,使
,使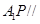 面
面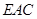 ?若存在,求
?若存在,求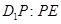 的值;不存在,说明理由.
的值;不存在,说明理由.
 平面
平面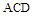 ,
,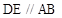 ,
,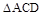 是正三角形,AD=DE
是正三角形,AD=DE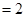 AB,且F是CD的中点.
AB,且F是CD的中点.