题目内容
若满足条件C=60°，AB=
，BC=a的△ABC有两个，那么a的取值范围是（ ）
| 3 |
A、（1，
| ||||
B、（
| ||||
C、(
| ||||
| D、（1，2） |
分析：由已知条件C的度数，AB及BC的值，根据正弦定理用a表示出sinA，由C的度数及正弦函数的图象可知满足题意△ABC有两个A的范围，然后根据A的范围，利用特殊角的三角函数值即可求出sinA的范围，进而求出a的取值范围．
解答：解：由正弦定理得：
=
，即
=
，
变形得：sinA=
，
由题意得：当A∈（60°，120°）时，满足条件的△ABC有两个，
所以
＜
＜1，解得：
＜a＜2，
则a的取值范围是（
，2）．
故选C
| AB |
| sinC |
| BC |
| sinA |
| ||||
|
| a |
| sinA |
变形得：sinA=
| a |
| 2 |
由题意得：当A∈（60°，120°）时，满足条件的△ABC有两个，
所以
| ||
| 2 |
| a |
| 2 |
| 3 |
则a的取值范围是（
| 3 |
故选C
点评：此题考查了正弦定理及特殊角的三角函数值．要求学生掌握正弦函数的图象与性质，牢记特殊角的三角函数值以及灵活运用三角形的内角和定理这个隐含条件．
练习册系列答案
相关题目
，∠C=60°的△ABC有两个解，则边长a的取值范围（ ）
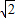，2）
，
）
，2）