题目内容
若满足条件c= ,∠C=60°的△ABC有两个解,则边长a的取值范围( )
,∠C=60°的△ABC有两个解,则边长a的取值范围( )A.(
 ,2)
,2)B.(
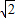 ,
, )
)C.(1,2)
D.(
 ,2)
,2)
【答案】分析:根据正弦定理,结合题中数据算出a=2sinA.再由0°<A<120°,讨论正弦函数图象在(0, )上的对应关系,发现x∈(
)上的对应关系,发现x∈(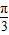 ,
,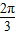 )且x
)且x 时,有两个A对应同一个sinA值,由此可得sinA的范围,从而得到边长a的取值范围.
时,有两个A对应同一个sinA值,由此可得sinA的范围,从而得到边长a的取值范围.
解答:解:∵△ABC中c= ,∠C=60°
,∠C=60°
∴由正弦定理 ,可得a=
,可得a= =2sinA
=2sinA
∵0°<A<120°,即A∈(0, )
)
在区间(0,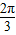 )上,当A∈(
)上,当A∈( ,
, )且A
)且A 时,有两个A对应同一个sinA值
时,有两个A对应同一个sinA值
∴当△ABC有两个解时, <sinA<1,可得a=2sinA∈(
<sinA<1,可得a=2sinA∈( ,2)
,2)
故选:A
点评:本题给出三角形的一边和它的对角,求三角形有两解时边a的取值范围.着重考查了正弦定理、三角函数的图象与性质等知识,属于基础题.
 )上的对应关系,发现x∈(
)上的对应关系,发现x∈(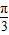 ,
,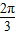 )且x
)且x 时,有两个A对应同一个sinA值,由此可得sinA的范围,从而得到边长a的取值范围.
时,有两个A对应同一个sinA值,由此可得sinA的范围,从而得到边长a的取值范围.解答:解:∵△ABC中c=
 ,∠C=60°
,∠C=60°∴由正弦定理
 ,可得a=
,可得a= =2sinA
=2sinA∵0°<A<120°,即A∈(0,
 )
)在区间(0,
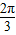 )上,当A∈(
)上,当A∈( ,
, )且A
)且A 时,有两个A对应同一个sinA值
时,有两个A对应同一个sinA值∴当△ABC有两个解时,
 <sinA<1,可得a=2sinA∈(
<sinA<1,可得a=2sinA∈( ,2)
,2)故选:A
点评:本题给出三角形的一边和它的对角,求三角形有两解时边a的取值范围.着重考查了正弦定理、三角函数的图象与性质等知识,属于基础题.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
若满足条件C=60°,AB=
,BC=a的△ABC有两个,那么a的取值范围是( )
| 3 |
A、(1,
| ||||
B、(
| ||||
C、(
| ||||
| D、(1,2) |