题目内容
(本题满分12分)已知函数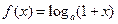 ,
,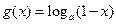 ,其中
,其中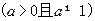 ,设
,设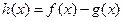
(1)判断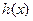 的奇偶性,并说明理由
的奇偶性,并说明理由
(2)若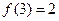 ,求使
,求使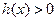 成立的x的集合
成立的x的集合
解:(1)依题意得1+x>0,1-x>0,
∴函数h(x)的定义域为(-1,1).………………………………………..………… ………………3分
………………3分
∵对任意的x∈(-1,1),-x∈(-1,1),
h(-x)=f(-x)-g(-x)
=loga(1-x)-loga(1+x)
=g(x)-f(x)=-h(x),
∴h(x)是奇函数. .................................................... ............
............ ..........................................6分
..........................................6分
(2)由f(3)=2,得a=2.
此时h(x)=log2(1+x)-log2(1-x),
由h(x)>0即log2(1+x)-log2(1-x)>0,
∴log2(1+x)>log2(1-x) .
.
由1+x>1-x>0,解得0<x<1.
故使h(x)>0成立的x的集合是{x|0<x<1}. ................................................................................12分
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知:函数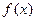 对一切实数
对一切实数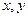 都有
都有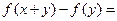
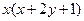 成立,且
成立,且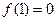 .
.
(1)求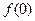 的值。
的值。
(2)求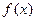 的解析式。
的解析式。
(3)已知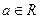 ,设P:当
,设P:当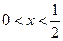 时,不等式
时,不等式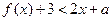 恒成立;Q:当
恒成立;Q:当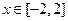 时,
时,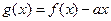 是单调函数。如果满足P成立的
是单调函数。如果满足P成立的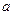 的集合记为
的集合记为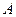 ,满足Q成立的
,满足Q成立的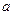 的集合记为
的集合记为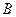 ,求
,求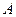 ∩
∩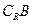 (
(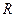 为全集)。
为全集)。
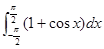 等于( )
等于( )
| A.π | B.2 | C.π﹣2 | D.π+2 |
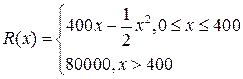 ,其中
,其中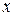 是仪器的月产量.
是仪器的月产量. ;
;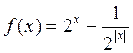
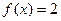 ,求
,求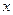 的值;
的值;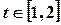 ,
,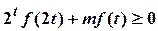 恒成立,求实数
恒成立,求实数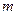 的取值范围。
的取值范围。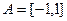 ,
,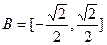 ,函数
,函数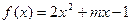 ,
,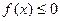 的解集为C,当
的解集为C,当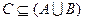 时,求实数
时,求实数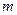 取值范围;
取值范围;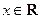 ,都有
,都有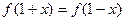 成立,试求
成立,试求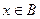 时,
时, 的值
的值 域;
域;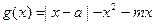
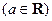 ,求
,求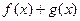 的最
的最 小值.
小值. 对
对 都满足
都满足 且
且 ,设函数
,设函数
 ,
, ).
). ,使
,使
 成立,求实数
成立,求实数 的取值范围;
的取值范围; ,
, ,求证:对于
,求证:对于 ,恒有
,恒有 .
.  是定义在
是定义在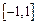 上的奇函数,当
上的奇函数,当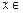
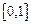 时,
时,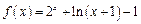 .
.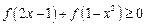 .
.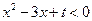 的解集为
的解集为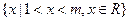 ;
; 的值;
的值;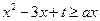 在
在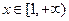 上恒成立,求实数
上恒成立,求实数 的最大值.
的最大值.