题目内容
(本小题满分15分)已知二次函数 对
对 都满足
都满足 且
且 ,设函数
,设函数
( ,
, ).
).
(1)求 的表达式;
的表达式;
(2)若 ,使
,使
 成立,求实数
成立,求实数 的取值范围;
的取值范围;
(3)设 ,
, ,求证:对于
,求证:对于 ,恒有
,恒有 .
.
解:(1)设 ,于是
,于是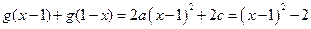 ,所以
,所以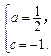
又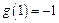 ,则
,则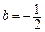 .所以
.所以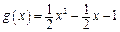 .
.
(2)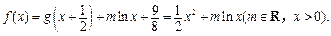
当m>0时,由对数函数性质,f(x)的值域为R;
当m=0时,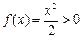 对
对 ,
,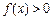 恒成立;
恒成立;
当m<0时,由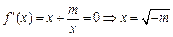 ,
,
列表:x 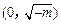
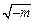
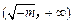

- 0 + 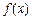
递减 极小值 递增
这时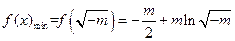 ,
,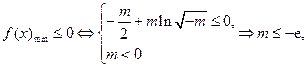
综上,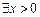 使
使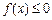 成立,实数m的取值范围
成立,实数m的取值范围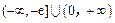 .
.
(3)由题知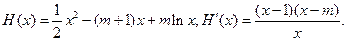 因为对
因为对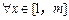 ,
,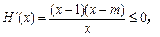 所以
所以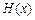 在
在 内单调递减.
内单调递减.
于是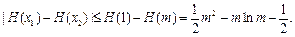
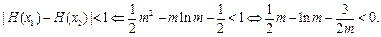
记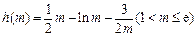 ,则
,则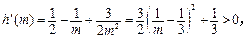
所以函数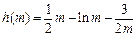 在
在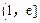 是单调增函数,
是单调增函数,
所以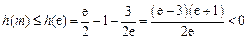 ,故命题成立.
,故命题成立.
解析

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
若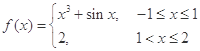 ,则
,则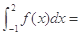 ( )
( )
| A.0 | B.1 | C.2 | D.3 |
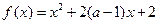 ,
, 的值域为
的值域为 ,求实数a的值;
,求实数a的值; 
 米,记∠BHE=θ.
米,记∠BHE=θ. ,求此时管道的长度L;
,求此时管道的长度L;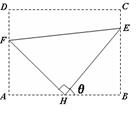
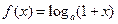 ,
,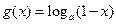 ,其中
,其中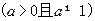 ,设
,设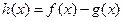
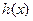 的奇偶性,并说明理由
的奇偶性,并说明理由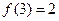 ,求使
,求使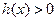 成立的x的集合
成立的x的集合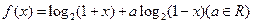 .
. )关于原点对称,求a的值;
)关于原点对称,求a的值;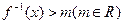 .
.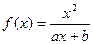 (a,b为常数)且方程f(x)-x+12=0
(a,b为常数)且方程f(x)-x+12=0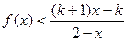 .
. 。已知2010年生产饮料的设备折旧
。已知2010年生产饮料的设备折旧 ,维修等固定费用为3 万元,每生产1万件
,维修等固定费用为3 万元,每生产1万件 成本—促销费,生产成本=固定费用+生产费用)
成本—促销费,生产成本=固定费用+生产费用)