题目内容
(本小题12分)设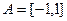 ,
,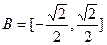 ,函数
,函数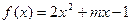 ,
,
(Ⅰ)设不等式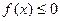 的解集为C,当
的解集为C,当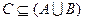 时,求实数
时,求实数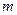 取值范围;
取值范围;
(Ⅱ)若对任意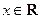 ,都有
,都有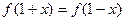 成立,试求
成立,试求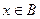 时,
时, 的值
的值 域;
域;
(Ⅲ)设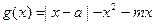
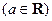 ,求
,求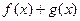 的最
的最 小值.
小值.
解:(1)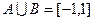 ,因为
,因为 ,二次函数
,二次函数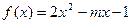 图像
图像
开口向上,且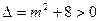 恒成立,故图像始终与
恒成立,故图像始终与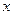 轴有两个交点,由题意,要使这两个
轴有两个交点,由题意,要使这两个
交点横坐标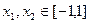 ,当且仅当:
,当且仅当: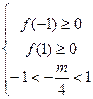 , 解得:
, 解得:

(2)对任意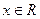 都有
都有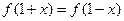 ,所以
,所以 图像关于直线
图像关于直线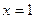 对称,
对称,
所以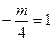 ,得
,得 .所以
.所以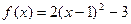 为
为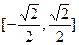 上减函数.
上减函数. 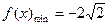 ;
;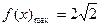 .故
.故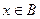 时,
时, 值域为
值域为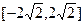 .
.
(3)令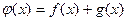 ,则
,则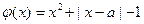
(i)当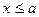 时,
时,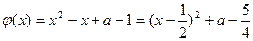 ,
,
当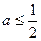 ,则函数
,则函数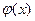 在
在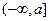 上单调递减,
上单调递减,
从而函数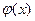 在
在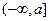 上的最小值为
上的最小值为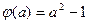 .
.
若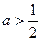 ,则函数
,则函数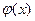 在
在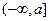 上
上 的最小值为
的最小值为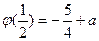 ,且
,且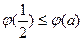 .
.
(ii) 当
当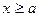 时,函数
时,函数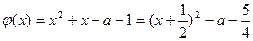
若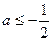 ,则函数
,则函数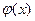 在
在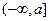 上的最小值为
上的最小值为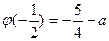 ,且
,且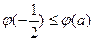
若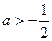 ,则函数
,则函数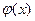 在
在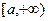 上单调递增,
上单调递增,
从而函数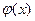 在
在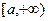 上的最小值为
上的最小值为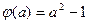 .
.
综上,当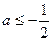 时,函数
时,函数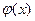 的最小值为
的最小值为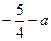
当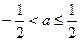 时,函数
时,函数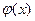 的最小值为
的最小值为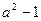
当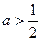 时,函数
时,函数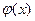 的最小值为
的最小值为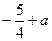
解析

练习册系列答案
相关题目
 ,(
,(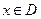 ),若同时满足以下条件:
),若同时满足以下条件: ]
]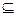 D,使
D,使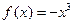 符合条件②的区间[
符合条件②的区间[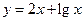 是不是闭函数?若是请找出区间[
是不是闭函数?若是请找出区间[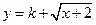 是闭函数,求实数
是闭函数,求实数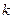 的取值范围.
的取值范围.
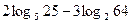
 米,记∠BHE=θ.
米,记∠BHE=θ. ,求此时管道的长度L;
,求此时管道的长度L;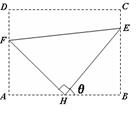

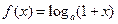 ,
,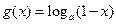 ,其中
,其中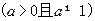 ,设
,设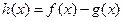
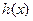 的奇偶性,并说明理由
的奇偶性,并说明理由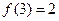 ,求使
,求使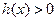 成立的x的集合
成立的x的集合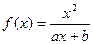 (a,b为常数)且方程f(x)-x+12=0
(a,b为常数)且方程f(x)-x+12=0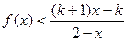 .
. ,
, ,函数
,函数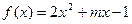
 的解集为C,当
的解集为C,当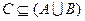 时,求实数
时,求实数 取值范围
取值范围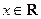 ,都有
,都有 成立,试求
成立,试求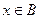 时,
时,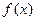 的值
的值 域
域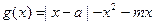
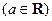 ,求
,求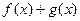 的最小值
的最小值