题目内容

19．已知集合A={x|y=$\sqrt{2-x}$}，B={x|3x-x2≥0}，则集合A∩B=（　　）
A．[0，2]B．[0，3]C．[0，2）D．（-∞，0]

分析 求出A中x的范围确定出A，求出B中不等式的解集确定出B，找出A与B的交集即可．

解答 解：由A中y=$\sqrt{2-x}$，得到2-x≥0，
解得：x≤2，即A=（-∞，2]，
由B中不等式变形得：x（x-3）≤0，
解得：0≤x≤3，即B=[0，3]，
则A∩B=[0，2]，
故选：A．

点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．

练习册系列答案
相关题目
9．在△ABC中，角A，B，C的对边分别是a、b、c，已知$\overrightarrow a=（{cosA，cosB}）$，$\overrightarrow b=（{a，2c-b}）$，且$\overrightarrow a∥\overrightarrow b$．
（Ⅰ）求角A的大小；
（Ⅱ）若b=3，△ABC的面积${S_{△ABC}}=3\sqrt{3}$，求a的值．
10．已知曲线C1的极坐标方程为ρ2cos2θ=8，曲线C2的极坐标方程为$θ=\frac{π}{6}$，曲线C1、C2相交于A、B两点．
（Ⅰ）求A、B两点的极坐标；
（Ⅱ）曲线C1与直线$\left\{\begin{array}{l}x=2+\frac{{\sqrt{3}}}{2}t\\ y=\frac{1}{2}t\end{array}\right.$（t为参数）分别相交于M，N两点，求线段MN的长度．
7．设D、E、F分别为△ABC三边BC、CA、AB的中点，则$\overrightarrow{DA}$+$\overrightarrow{EB}$+$\overrightarrow{FC}$=（　　）
A．$\frac{1}{2}$$\overrightarrow{DA}$B．$\frac{1}{3}$$\overrightarrow{DA}$C．$\frac{1}{4}$$\overrightarrow{DA}$D．$\overrightarrow{0}$
14．已知数列{an}的前n项和为Sn，且对任意正整数n，都有3an=2Sn+3成立．
（1）求数列{an}的通项公式；
（2）设bn=log3an，求数列{bn}的前n项和Tn．
4．函数f（x）=（$\frac{2}{1+{e}^{x}}$-1）sinx的图象的大致形状是（　　）
A．B．C．D．
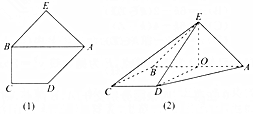11．如图（1），在五边形BCDAE中，CD∥AB，∠BCD=90°，CD=BC=1，AB=2，△ABE是以AB为斜边的等腰直角三角形，现将△ABE沿AB折起，使平面ABE⊥平面ABCD，如图（2），记线段AB的中点为O．
（Ⅰ）求证：平面ABE⊥平面EOD；
（Ⅱ）求平面ECD与平面ABE所成的锐二面角的大小．
8．已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左焦点F1与抛物线y2=-4x的焦点重合，椭圆E的离心率为$\frac{\sqrt{2}}{2}$，过点M （m，0）（m＞$\frac{3}{4}$）作斜率不为0的直线l，交椭圆E于A，B两点，点P（$\frac{5}{4}$，0），且$\overrightarrow{PA}$•$\overrightarrow{PB}$为定值．
（Ⅰ）求椭圆E的方程；
（Ⅱ）求△OAB面积的最大值．
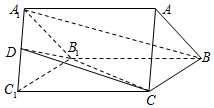20．如图，在三棱柱ABC-A1B1C1中，△ABC是等边三角形，BC=CC1，D是A1C1中点．
（Ⅰ）求证：A1B∥平面B1CD；
（Ⅱ）当三棱锥C-B1C1D体积最大时，求点B到平面B1CD的距离．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网