题目内容
（17）已知三点P（5，2）、
（－6，0）、
（6，0）. （Ⅰ）求以
、
为焦点且过点P的椭圆的标准方程；
（Ⅱ）设点P、
、
关于直线y＝x的对称点分别为
、
、
，求以
、
为焦点且过点
的双曲线的标准方程。
本小题主要考查椭圆与双曲线的基本概念、标准方程、几何性质等基础知识和基本运算能力.
解：（Ⅰ）由题意，可设所求椭圆的标准方程为
其半焦距c=6.
∴a=3,b2=a2-c2=45-36=9.
所以所求椭圆的标准方程
（Ⅱ）点P（5，2）、F1（-6，0）、F2（6，0）关于直线y=x的对称点分别为P′（2，5）、F′1（0，-6）、F′2（0，6）.
设所求双曲线的标准方程为
由题意知，半焦距c1=6，
∴a1=2，b21=c21-a21=36-20=16.
所以所求双曲线的标准方程为
练习册系列答案
相关题目
OP是底部O不能到达的高塔，P是高塔的最高点，选择一条水平基线M，N，使得M，N，O三点在同一条直线上，在相距为d的M，N两点用测角仪测得P的仰角分别为α，β，已知测角仪高h=1.5m，试完成如下《实验报告》
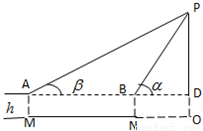
（要求：（1）计算两次测量值的平均值并填入表格；（2）利用α，β，d的平均值，求OP的值，写出详细的计算过程；
（3）把计算结果填入表格．（相关数据：）
（要求：（1）计算两次测量值的平均值并填入表格；（2）利用α，β，d的平均值，求OP的值，写出详细的计算过程；
（3）把计算结果填入表格．（相关数据：）
| 题目 | 测量底部不能到达的高塔的高度 | 计算过程 | |||
| 测量数据 | 测量项目 | 第一次 | 第二次 | 平均值 | |
| α | 75°32′ | 74°28′ | |||
| β | 30°17′ | 29°43′ | |||
| d（m） | 59.82 | 60.18 | |||
| 测量目标 | |||||
| 结果 | |||||