题目内容
若|z|=1，则|z+i|+|z-6|的最小值等于 ．
考点：复数的代数表示法及其几何意义
专题：数系的扩充和复数
分析：满足|z|=1的复数z，在以原点为圆心，以1为半径的圆上，|z+i|+|z-6|表示复数z在复平面内对应点Z到点A（0，-1）和B（6，0）的距离之和，根据复数的几何意义进行求解即可．
解答：
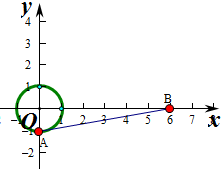解：满足|z|=1的复数z，在以原点为圆心，以1为半径的圆上，|z+i|+|z-6|表示复数z在复平面内对应点Z到点A（0，-1）和B（6，0）的距离之和，
作出对应的图象如图：
则由图象知Z位于A时，|z+i|+|z-6|取得最小值，最小值为|AB|=
=
，
故答案为：
解：满足|z|=1的复数z，在以原点为圆心，以1为半径的圆上，|z+i|+|z-6|表示复数z在复平面内对应点Z到点A（0，-1）和B（6，0）的距离之和，作出对应的图象如图：
则由图象知Z位于A时，|z+i|+|z-6|取得最小值，最小值为|AB|=
| 1+62 |
| 37 |
故答案为：
| 37 |
点评：本题主要考查复数的几何意义的应用，利用数形结合是解决本题的关键．
练习册系列答案
相关题目
设a=40.1，b=log30.1，c=0.50.1，则（ ）
| A、a＞b＞c |
| B、a＞c＞b |
| C、b＞a＞c |
| D、b＞c＞a |
已知全集U={0，1，2，3，4，5，6}，集合A={0，1，2，3}，B={3，4，5}，则（∁UA）∩B=（ ）
| A、{3} |
| B、{4，5} |
| C、{4，5，6} |
| D、{0，1，2} |
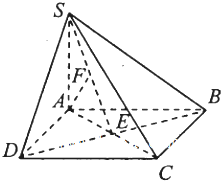如图，在四棱锥S-ABCD中，底面ABCD为正方形，AS⊥平面ABCD，函数y=
的最大值是（ ）
|
| A、3 | B、4 | C、5 | D、6 |