题目内容
10.已知函数g(x)是定义在区间[-3-m,m2-m]上的偶函数(m>0),且f(x)=$\left\{\begin{array}{l}{{x}^{2}+1,(x<0)}\\{f(x-|m|),(x≥0)}\end{array}\right.$,则f(2016)=( )| A. | 1 | B. | 2 | C. | 9 | D. | 10 |
分析 根据函数奇偶性的定义域的对称性求出m,利用函数的周期性进行转化求解即可.
解答 解:∵函数g(x)是定义在区间[-3-m,m2-m]上的偶函数(m>0),
∴-3-m+m2-m=0,
即m2-2m-3=0,
得m=3或m=-1,
∵m>0,
∴m=3,
则当x≥0时,f(x)=f(x-3),
则f(2016)=f(672×3)=f(0)=f(-3)=(-3)2+1=9+1=10,
故选:D.
点评 本题主要考查函数值的计算,根据条件求出m的值,然后根据分段函数进行转化求解是解决本题的关键.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
2.曲线y=$\frac{1}{2}$x2-2x在x=3处的切线的倾斜角为( )
| A. | 45° | B. | -45° | C. | 135° | D. | -135° |
1.已知a,b为异面直线,下列结论不正确的是( )
| A. | 必存在平面α使得a∥α,b∥α | |
| B. | 必存在平面α使得a,b与α所成角相等 | |
| C. | 必存在平面α使得a?α,b⊥α | |
| D. | 必存在平面α使得a,b与α的距离相等 |
5.在平面直角坐标系xOy中,已知△ABC的顶点A(0,3)和C(0,-3),顶点B在椭圆$\frac{x^2}{16}+\frac{y^2}{25}$=1上,则$\frac{sin(A+C)}{sinA+sinC}$=( )
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{5}{4}$ | D. | $\frac{5}{3}$ |
15.根据如下样本数据
求得y关于x的线性回归直线方程为$\widehat{y}$=2.1x+0.85,则m的值为0.5.
| x | 0 | 1 | 4m | 3 |
| y | m | 3 | m+5 | 7 |
2.已知数列{an}的前n项和为Sn,若Sn=2an-4,n∈N*,则an=( )
| A. | 2n+1 | B. | 2n | C. | 2n-1 | D. | 2n-2 |
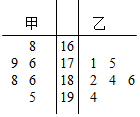 在一次水稻试验田验收活动中,将甲、乙两种水稻随机抽取各6株样品,单株籽粒数制成如图所示的茎叶图:
在一次水稻试验田验收活动中,将甲、乙两种水稻随机抽取各6株样品,单株籽粒数制成如图所示的茎叶图: